6. Корреляционный анализ и регрессионный анализ данных

6.1. Корреляционный анализ

Корреляционный анализ – это совокупность методов обнаружения так называемой корреляционной зависимости между случайными величинами.

Для двух случайных величин Х и Y корреляционный анализ состоит из следующих этапов:

-        построение корреляционного поля и составление корреляционной таблицы;

-        вычисление выборочного коэффициента корреляции;

-        проверка статической гипотезы о значимости корреляционной связи.

Рассмотрим подробнее каждый из указанных этапов.

Корреляционное поле и корреляционная таблица являются исходными данными при корреляционном анализе. Пусть , , – результаты парных наблюдений над случайными величинами Х и Y. Изображая полученные результаты в виде точек в декартовой системе координат, получим корреляционное поле. По характеру расположения точек поля можно составить предварительное представление о форме зависимости случайных величин (например, о том, что одна из них в среднем возрастает или убывает с возрастанием другой).

Пример 6.1. Исследование зависимости между среднемесячными доходами X на семью (в тыс. у.е.) и расходами Y на покупку кондитерских изделий (в у.е.) представлено в таблице:

Построить корреляционное поле и сделать предварительный вывод о форме зависимости случайных величин.

Решение. Корреляционное поле, построенное по статистическим данным, приведено на рис. 6.1.

Рис. 6.1.

Анализ рис. 6.1 позволяет сделать вывод о наличии сильной линейной статистической связи между среднемесячными доходами семьи и затратами на приобретение ею кондитерских изделий. При этом связь имеет положительную тенденцию, т.е. с ростом переменной X наблюдается увеличение отклика Y.

При большом объеме выборки результаты группируются и представляются в виде корреляционной таблицы.

Пример 6.2. По 20 туристическим фирмам были установлены затраты X на рекламу и количества туристов Y, воспользовавшихся услугами каждой фирмы. В таблице фирмы ранжированы по величине затрат на рекламу:

Построить корреляционную таблицу и сделать предварительный вывод о форме зависимости случайных величин.

Решение. Исходные данные, ранжированные по величине затрат на рекламу, уже могут быть использованы при ответе на вопрос о наличии или отсутствии корреляционной связи. Этот простейший прием обнаружения связи называется сопоставлением двух параллельных рядов. Согласно этому элементарному приему, значения факторного признака X располагают в неубывающем порядке и затем прослеживают направление изменения результативного признака Y.

По таблице можно видеть, что в целом для всей совокупности фирм увеличение затрат на рекламу приводит к увеличению количества туристов, пользующихся услугами фирмы. Хотя в отдельных случаях наличие такой зависимости может не усматриваться. Например, сопоставим данные по фирмам с порядковыми номерами 7 и 11. Здесь можно увидеть даже обратное соотношение: у фирмы 11 количество туристов меньше, чем у фирмы 7, хотя затраты на рекламу выше. В каждом отдельном случае количество туристов, воспользовавшихся услугами фирмы, будет зависеть не только от размера затрат фирмы на рекламу, но и от того, как сложатся прочие факторы, определяющие величину результативного признака.

Однако наличие большого числа различных значений результативного признака, соответствующих одному и тому же значению признака-фактора, затрудняет восприятие таких параллельных рядов. Особенно это сказывается при большом числе единиц, составляющих изучаемую совокупность. В таких случаях целесообразнее воспользоваться для установления факта наличия связи корреляционной таблицей. Построение корреляционной таблицы начинают с группировки значений факторного и результативного признаков. Поскольку в приводимом примере факторный признак представлен всего пятью вариантами повторяющихся значений, достаточно в первом столбце корреляционной таблицы выписать эти результаты. Для результативного признака необходимо определить величину интервала группировки. Это можно сделать с помощью формулы Стержэсса:

.

В корреляционной таблице факторный признак X, как правило, располагают в строках, а результативный признак Y – в столбцах таблицы. Числа, расположенные на пересечении строк и столбцов таблицы, означают частоту повторения данного значения X и Y:

Данная корреляционная таблица уже при общем знакомстве дает возможность выдвинуть предположение о наличии или отсутствии связи, а также выяснить ее направление. Если частоты в корреляционной таблице расположены на диагонали из левого верхнего угла в правый нижний угол (т.е. бóльшим значениям фактора соответствуют бóльшие значения функции), то можно предположить наличие прямой корреляционной зависимости между признаками. Если же частоты расположены по диагонали из правого верхнего угла в левый нижний, то предполагают наличие обратной связи между признаками.

Необходимо подчеркнуть, что при рассмотрении корреляционной таблицы важно установить расположение основной части частот. Возможны варианты, когда все клетки корреляционной таблицы окажутся заполненными. Однако это обстоятельство еще не означает, что корреляционная связь между признаками отсутствует. Нужно установить, как расположена в таблице основная масса частот. Для того, чтобы сделать восприятие корреляционной таблицы более доступным и в целях более четкого выявления основной тенденции связи, можно для каждой строки рассчитать средние значения  результативного признака Y, соответствующие определенному значению признака-фактора X. Так, в рассматриваемом примере среднее число туристов для первой группы, состоящей из трех фирм, которые тратят на рекламу 8 усл. ден. ед., будет равно 800 человек:

.

Для следующей группы, состоящей из пяти фирм, у которых затраты на рекламу 9 усл. ден. ед.

,

и т.д. (рассчитанные таким образом средние  представлены в последнем столбце корреляционной таблицы).

Итак, увеличение средних значений результативного признака с увеличением значений факторного признака еще раз свидетельствует о возможном наличии прямой корреляционной зависимости числа туристов, воспользовавшихся услугами фирмы, от затрат фирмы на рекламу.

Корреляционная таблица позволяет сжато, компактно изложить материал. Поэтому все последующие расчеты можно вести по корреляционной таблице.

 

Выборочный коэффициент корреляции Пирсона для группированной  корреляционной таблицы определяется формулой:

,                                                     (6.1)

где

                                          (6.2)

– выборочная ковариация;  и  – центры соответствующих интервалов группировки;

, ,

,                            (6.3)

– соответствующие выборочные дисперсии.

Для выборочной ковариации  справедлива формула

,                               (6.4)

являющаяся аналогом формулы  в теории вероятностей. Для простой (негруппированной) выборки формулы (6.2) – (6.4) упрощаются и приобретают вид:

,                                          (6.5)

,

, .                             (6.6)

Выборочный коэффициент корреляции  обладает всем свойствами, которыми обладает теоретико-вероятностный коэффициент корреляции . В частности, для любой выборки .

При этом, чем ближе  к 1 (или к ), тем сильнее выражена линейная зависимость между X и Y. Однако значимость такой зависимости должна быть

подкреплена проверкой гипотезы. Проверка гипотезы о наличии корреляции осуществляется следующим образом. Основная гипотеза – отсутствие линейной статистической связи (); альтернативной гипотезой может выступать любая из трех возможных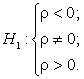

В тех случаях, когда справедливо предположение о нормальном распределении двумерного генерального вектора , подходящей статистикой для проверки основной гипотезы является статистика Стъюдента

,                                                 (6.7)

где обозначено  – выборочный коэффициент корреляции, а объем n выборки предполагается большим (число степеней свободы равно ).

Пример 6.3. В таблице представлены результаты измерений роста Х (см) и веса Y (кг) 50 мужчин – слушателей военной академии:

Вычислить выборочный коэффициент корреляции и проверить гипотезу о значимости корреляционной связи.

 По формулам группированной выборки вычисляем средние

, ,

выборочные вторые начальные моменты

, , .

Далее, используя формулы (6.2) – (6.4), получаем:

, , .

Наконец, по формуле (6.1) определяем:

.

Проверим значимость коэффициента корреляции при двусторонней альтернативе () и . Из таблицы распределения Стъюдента находим квантиль . Выборочное значение статистики Z равно:

.

Так как , то , поэтому гипотеза  отклоняется в пользу гипотезы . Корреляция значима.

Замечание. Несколько обескураживающий результат предыдущего примера( отвергнута при достаточно малом значении r) объясняется сильной зависимостью статистики Стъюдента от объема выборки n. В следующем параграфе при анализе регрессии будет показано, что линейная связь может оказаться значимой и при малых значениях коэффициента корреляции r. Однако для получения надежных выводов при использовании статистики Z следует иметь более 100 наблюдений.

Менее чувствительной к объему выборки является статистика U, основанная на преобразовании Фишера:

.

Фишером было доказано, что при  случайная величина V имеет приближенно нормальное распределение с независящей от r дисперсией

,

и математическим ожиданием

,

где  – истинное (но неизвестное) значение коэффициента корреляции двумерного генерального вектора .

Стандартизуя V, получим подходящую статистику Фишера:

.                                             (6.8)

Заметим, что с помощью указанной статистики можно проверять более общую гипотезу о сравнении с эталоном  против любой из трех альтернатив . В этом случае  заменяется на условное математическое ожидание

,

центрирование статистики V в формуле (6.8) осуществляется на эту величину.

Пример 6.4. Проведены парные измерения производительности труда Y в зависимости от уровня механизации работ X для 28 промышленных предприятий Московской области. В результате получен выборочный коэффициент корреляции . Решить следующие две задачи.

1)     В условиях двусторонней альтернативы  найти критическое значение уровня значимости , такое, что при  гипотеза  будет приниматься для полученного в данной выборке коэффициента корреляции.

2)     Для  и правосторонней альтернативы  найти критическое значение  такое, что при  гипотеза  будет отвергаться в пользу .

 1) Воспользуемся статистикой Фишера (6.8). Так как  (проверяется значимость коэффициента корреляции), то , поэтому статистика U принимает вид:

.

Вычислим

.

Примем полученное значение за критическую точку, определяемую как квантиль  из нормального распределения. Из таблицы нормального распределения, полагая , находим: .

Таким образом, при  гипотеза  для данного значения  будет приниматься.

2) Пусть . По таблице нормального распределения находим квантиль . Отсюда следует, что при  гипотеза  будет отклонена.

Решая неравенство  относительно r, получим условие отклонения гипотезы  в пользу гипотезы : .

 

6.2. Регрессионный анализ

Зависимость между случайными величинами X и Y называется стохастической, если с изменением одной их них (например, Х) меняется закон распределения другой (Y). В качестве примеров такой зависимости приведем зависимость веса человека (Y) от его роста (Х), предела прочности стали (Y) от ее твердости (Х) и т.д.

В теории вероятностей стохастическую зависимость Y от Х описывают условным математическим ожиданием:

которое, как видно из записи, является функцией от независимой переменной х , имеющей смысл возможного значения случайной величины Х.

Уравнение  называется уравнением регрессии Y на x. Переменная х называется регрессионной переменной или регрессором. График функции  называется линией или кривой регрессии. Кривые регрессии обладают следующим свойством: среди всех действительных функций  минимум  достигается для функции

,

т.е. регрессия Y на x дает наилучшее в среднеквадратическом смысле предсказание величины Y по заданному значению . На практике это используется для прогноза Y по Х: если непосредственно наблюдаемой величиной является лишь компонента Х случайного вектора  (например, Х – диаметр сосны), то в качестве прогнозируемого значения Y (высота сосны) берется условное математическое ожидание . Наиболее простым является случай, когда регрессия Y на x линейна:

.

Если  – случайный вектор, распределенный по двумерному нормальному закону, то коэффициенты  и определяются равенствами:

, ,

уравнением регрессии в этом случае является прямая линия

,

проходящая через центр рассеивания  с угловым коэффициентом , называемым коэффициентом регрессии Y на x.

В реальных экспериментах, связанных со статической обработкой опытных данных, условный закон распределения случайной величины Y при условии  обычно заранее неизвестен. В таком случае, речь может идти лишь о каком либо приближении к теоретической кривой регрессии, построенном на основе выборочных данных. Другими словами, задача заключается в подборе подходящей функциональной зависимости, наилучшим образом (в некотором статистическом смысле) приближающей стохастическую зависимость.

Во многих случаях можно считать, что «независимая» переменная Х находится под контролем экспериментатора, и может бать измерена с любой заданной точностью, в то время как измеряемые значения Y как функции от Х (выборочные значения  при фиксированных ) определяются с ошибкой (содержат шум измерения). Если вид функциональной зависимости зафиксирован, то статистическую модель регрессии можно записать следующим образом:

                                      (1)

где  – набор неизвестных параметров, определяющих функциональную зависимость (параметры регрессии);  – случайные величины, складывающиеся при каждом фиксированном  из шума измерений и ошибки модели. При исследовании качества построения модели важно уметь разделять эти ошибки.

Следует иметь в виду, что наличие шума измерения делает невозможной задачу интерполяции, т.е. график искомой зависимости не должен проходить через все выборочные точки, а должен проходить таким образом, чтобы «сгладить» шум. Поскольку уровень шума определяется дисперсией , то задача состоит в подборе параметров , которые минимизируют . В действительности минимизируется не сама дисперсия (она неизвестна), а ее выборочная оценка, которая, как будет показано ниже, пропорциональна сумме квадратов отклонений (по оси Оу) кривой регрессии от соответствующих выборочных значений , т.е. пропорциональна величине

²

Указанный критерий минимизации суммы квадратов отклонений носит название метода наименьших квадратов (сокращенно МНК), а полученные в результате решения этой задачи оценки  параметров называются МНК-оценками. Основанием для выбора критерия МНК служит следующая теорема.

Теорема. Пусть в модели регрессии (1) случайные величины , , независимы в совокупности и одинаково распределены по закону  (физически условие , , означает, что измерения проводятся с одинаковой точностью). Тогда МНК-оценки  параметров регрессии совпадают с оценками максимального правдоподобия.

 Заметим, что по условию теоремы

, ,

поэтому наблюдаемые значения  одинаково распределены по закону . Так как  независимы в совокупности, то функция правдоподобия выборки запишется в виде

.

Из этого выражения следует, что

,

что и требовалось доказать.

Замечание. На практике ошибки измерений часто удовлетворяют поставленным в теореме условиям в силу центральной предельной теоремы.

Регрессионный анализ проводится в три этапа.

На первом этапе по характеру корреляционного поля выдвигают гипотезу о виде функциональной зависимости . Довольно часто используют следующее представление для функции :

,

где  – известные координатные функции. Такая модель регрессии называется линейной по параметрам. В частном случае, когда , модель называется полиномиальной.

На втором этапе по имеющимся выборочным данным осуществляют подгонку модели, т.е. находят МНК-оценки неизвестных параметров регрессии .

На третьем этапе анализируют качество построения модели: проверяются так называемые корректность и адекватность модели. Этот этап осуществляется средствами проверки статистических гипотез.

Пример 1. Построение прямой регрессии Y на x.

Пусть получена выборка , , из двумерного распределения . Корреляционный анализ показал, что корреляционная связь Y на x значима на некотором уровне . Выдвигается гипотеза о том, что уравнение прямой регрессии

должно хорошо аппроксимировать стохастическую зависимость Y на x. Найти МНК-оценки параметров а и b.

 Пусть задан план эксперимента, т.е. совокупность точек . Выбор этих точек – отдельная задача, решаемая в рамках теории оптимального планирования эксперимента и на данном этапе не обсуждается. Часто точки  распределяют эквидистантно, перекрывая интересующий нас интервал на оси Ох.

Искомые оценки являются решениями следующей задачи минимизации:

.

Применим классический метод поиска безусловного экстремума дифференцируемой функции . Запишем необходимые условия экстремума:

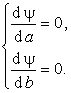
Получаем следующую систему линейных алгебраических уравнений для неизвестных значений а и b:

Деля обе части на n и вводя обычные обозначения для выборочных характеристик случайного вектора , приводим данную систему к виду

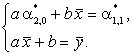                                                     (2)

где  – начальный выборочный момент порядка ,  и  – средние значения соответствующих переменных.

Решение системы (2), как нетрудно убедиться, имеет вид:

, ,

где  – выборочный коэффициент корреляции,  и  – выборочные среднеквадратические отклонения.

Уравнение линейной регрессии приобретает вид:

                                             (3)

Заметим, что полученное уравнение аналогично теоретическому уравнению регрессии, если заметить все входящие в него вероятностные моменты соответствующими выборочными оценками в соответствии с методом подстановки.

 

6.3 Однофакторный дисперсионный анализ

Пусть имеется l независимых нормальных совокупностей  с одной и той же, хотя и неизвестной, дисперсией . Математические ожидания  также неизвестны, но имеются основания предполагать, что они равны. Требуется поверить основную гипотезу  против альтернативы . Для этого из каждой совокупности (подпопуляции)  взята выборка объема :

, .

Формулируется следующая линейная модель дисперсионного анализа:

 – j-е наблюдение из i-ой подпопуляции,

 – среднее i-ой подпуляции,

 – генеральное (тотальное) среднее всей популяции X,

 – дифференциальный эффект, определяющий различие средних.

Интерпретация. Можно считать, что существует некоторый фактор A, имеющий l уровней, воздействие которого приводит к расщеплению всей популяции X на l подпопуляций , . Например, если измерения проводятся на l различных приборах, то можно исследовать влияние фактора «прибор» на результаты измерений. Термин «дисперсионный анализ» был первоначально предложен Р. Фишером (1925) для обработки результатов агрономических опытов, целью которых было выявление условий, позволяющих максимизировать урожай. Современные приложения дисперсионного анализа охватывают широкий круг задач техники, экономики, социологии, биологии, медицины и трактуются в терминах статистической теории проверки гипотез.

Заметим, что если дифференциальные эффекты  малы, то отклонение средних значений отдельных подпопуляций от тотального среднего можно рассматривать как случайное отклонение, и гипотеза  с большой вероятностью будет принята. Если , то получается уже известная нам задача проверки гипотезы о равенстве средних двух независимых нормальных совокупностей.

Напомним, что для проверки этой гипотезы использовалась статистика Стъюдента W, основанная на нормированной разности выборочных средних. Фишером доказано, что при  подходящей статистикой для проверки указанной гипотезы является фишеровское отношение дисперсий, сконструированных специальным образом.

Обозначим выборочное среднее i-ой выборки:

;                                                           (1)

общее среднее объединенной выборки:

;

объем объединенной выборки:

.

Легко видеть, что

,                                        (2)

т.е. тотальное среднее равно среднему арифметическому внутригрупповых средних.

Обозначим через сумму квадратов отклонений результатов наблюдений от общего среднего

.

Очевидно, что

является несмещенной оценкой неизвестной дисперсии , и кроме того,  являются несмещенными и состоятельными оценками математического ожидания .

Если гипотеза  верна, то  не должны сильно отличаться от общего среднего , но для точного решения задачи нужна подходящая статистика. Идея ее построения основана на разбиении суммы квадратов:

,

где

                                                  (3)

– сумма квадратов отклонений «внутри групп»,

                                              (4)

– сумма квадратов отклонений «внутри групп».

Покажем, как получается это разбиение. Преобразуем разность:

.

Возведем в квадрат:

.

Далее обе части равенства необходимо просуммировать сначала по k от 1 до , затем по i от 1 до l. Учтем, что согласно (1):

.

Поэтому

.

Выражение для этих сумм можно преобразовать к виду более удобному для вычислений:

,

.

Теорема. Если  независимы в совокупности, , и справедлива гипотеза , то  и  независимы, причем  распределена по закону , а  – по закону .

Из этой теоремы и теоремы Фишера следует, что статистика

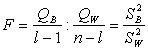
распределена по закону Фишера . Нетрудно убедиться, что F является подходящей статистикой для проверки гипотезы . Действительно, если гипотеза  верна, то величины  и  являются независимыми несмещенными оценками одного и того же параметра . Поэтому , что приводит к событию . Если же верна , то разброс между группами будет значительно больше, чем разброс внутри групп, т.е. , что приведет к попаданию  в критическую область, и основная гипотеза  будет с большой вероятностью отвергнута.

Пример 1. Три группы водителей обучались по различным методикам. По окончанию срока обучения был произведен тестовый контроль над случайно отобранными водителями из каждой группы. Результаты контроля сведены в следующую таблицу:

На уровне значимости  проверить гипотезу об отсутствии различий в результатах, получаемых по различным методикам.

 В данном случае фактор А – «методика обучения» имеет 3 уровня:

, .

По формуле (2) вычисляем тотальное среднее выборки: . Далее по формулам (3) и (4) находим , .

Отсюда

.

По таблице квантилей распределения Фишера находим критическую область . Отсюда .

Поскольку , то гипотеза  отклоняется в пользу . Фактор «методика обучения» приводит к значимым результатам в практике вождения автомобиля.