2.3. Функции случайных величин

2.3.1. Функции одномерных случайных величин

Пусть на вероятностном пространстве (, F, P) задана случайная величина X. Предположим, что имеется числовая функция  скалярного аргумента x. Случайную величину  назовем функцией от одномерной случайной величины X. Покажем, как построить закон распределения функции , зная закон распределения случайного аргумента X.

1. Пусть случайная величина X является дискретной.

Функция  от СВДТ X снова является дискретной случайной величиной, принимающей значения  с вероятностями , где  – множество возможных значений СВДТ X. Тогда для нахождения функции распределения можно воспользоваться соотношением

.

Однако, как правило, удобнее вначале составить ряд распределения случайной величины . Чтобы его построить, необходимо объединить в один столбец все одинаковые значения , приписав этому столбцу суммарную вероятность.

 

Пример 2.3.1. Закон распределения случайной величины X имеет вид:

Рассмотрим две числовые функции  и . Подставляя вместо аргумента x случайную величину Х, получим новые случайные величины  и . Построить ряды распределений случайных величин: 1) , 2) . Составить их функции распределения.

Решение. 1) Найдем возможные значения случайной величины Y:

, , , .

Тогда ряд распределения случайной величины Y имеет вид:

Составим теперь функцию распределения случайной величины :

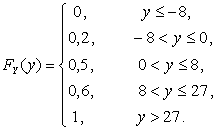
2) Найдем вначале значения функции :

, , , .

Значит, случайная величина Z имеет три возможных значения:

, , .

Вероятность возможного значения  равна сумме вероятностей несовместных событий  и , т.е. . Поэтому ряд распределения случайной величины Z имеет вид:

Составим теперь функцию распределения случайной величины :

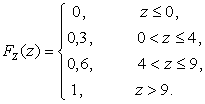
Ответ: 1) 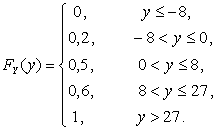 2) 

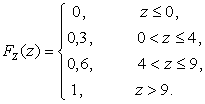
2. Пусть случайная величина X является непрерывной.

Рассмотрим вначале случайную величину , где  – гладкая строго монотонная функция скалярного аргумента x, а X – СВНТ с плотностью . Тогда плотность распределения  случайной величины Y находится по формуле:

,

где  – обратная по отношению к  функция.

Если же  – немонотонная функция на множестве возможных значений X, то следует разбить этот промежуток на такие интервалы, в которых функция  монотонна, и найти плотности распределений  для каждого из интервалов монотонности, а затем представить  в виде суммы

.

В частности, если функция  монотонна в двух интервалах, в которых соответствующие обратные функции равны  и , то

.

Пример 2.3.2. Найти плотность распределения СВНТ  (), где СВНТ X имеет плотность .

Решение.  при  гладкая строго монотонная функция. Тогда обратная функция . Отсюда . Таким образом,

.

Ответ: .

 

Пример 2.3.3. Случайная величина X распределена нормально с параметрами m и  (). Доказать, что линейная функция , где , также распределена нормально, причем , .

Решение. Напишем плотность распределения случайной величины X:

.

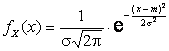Применим формулу , выведенную в предыдущем примере 2.3.2. Получим

.

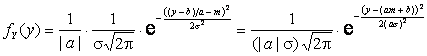Отсюда видно, что .

 

Пример 2.3.4. Случайная величина X распределена по закону Коши

.

Найти плотность распределения случайной величины .

Решение.  гладкая строго монотонная функция. Тогда обратная функция . Отсюда 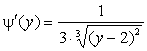, причем . Значит, .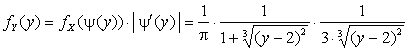

Таким образом,

.

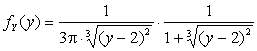Ответ: .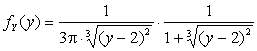

 

Пример 2.3.5. Случайная величина X распределена равномерно в интервале  (). Найти плотность распределения случайной величины .

Решение. Найдем плотность распределения  случайной величины X:

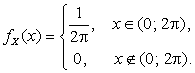
Из уравнения  найдем обратную функцию . Поскольку в интервале  функция  немонотонна, то необходимо разбить этот интервал на интервалы  и , в которых эта функция монотонна. На интервале  обратная функция , на интервале  обратная функция . Тогда искомая плотность распределения может быть найдена из равенства

.

Найдем производные обратных функций:

, .

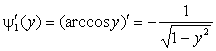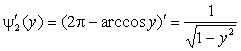Тогда модули производных равны

, .

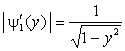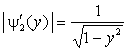Учитывая, что  при , получим

, .

Отсюда

.

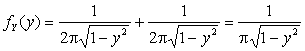Так как  при , то . Таким образом, на интервале  искомая плотность распределения равна 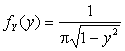, вне этого интервала .

Ответ: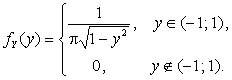

Рассмотрим далее на примерах, как находится функция распределения  случайной величины , если известна функция распределения  случайной величины X.

 

Пример 2.3.6. Задана функция распределения  случайной величины X. Найти функцию распределения  случайной величины , если: 1) ; 2) .

Решение. 1) По определению функции распределения . Поскольку функция  – возрастающая, то неравенство  выполняется, если имеет место неравенство , поэтому

.

Из уравнения  выразим x: . Тогда

.

2) По определению функции распределения . Поскольку функция  – убывающая, то неравенство  выполняется, если имеет место неравенство , поэтому

.

Из уравнения  выразим x: . Тогда

.

Ответ: 1) ; 2) .

 

2.3.2. Числовые характеристики функций одномерных случайных величин

Если X – случайная величина с известным законом распределения и , где  – неслучайная функция скалярного аргумента x, то математическое ожидание и дисперсия случайной величины Y (если они существуют) могут быть найдены по следующим формулам:

, если X – СВДТ,

, если X – СВНТ;

, если X – СВДТ,

, если X – СВНТ.

Аналогичные формулы имеют место и для всех прочих начальных и центральных моментов распределения случайной величины .

Замечание 1. Таким образом, для вычисления числовых характеристик функции одномерной случайной величины X необязательно знать закон распределения случайной величины , а достаточно знать закон распределения случайного аргумента X.

Замечание 2. Если , то математическое ожидание случайной величины  есть не что иное, как начальный момент s-го порядка, т.е.

.

Аналогично, если , то математическое ожидание случайной величины  есть центральный момент s-го порядка, т.е.

.

 

Пример 2.3.7. Закон распределения случайной величины X имеет вид:

Вычислить  и , если .

Решение. 1 способ (с помощью составления закона распределения случайной величины Y). Ряд распределения случайной величины Y имеет вид:

Тогда

;

.

2 способ (с помощью формул  и ):

;

.

Ответ: , .

 

Пример 2.3.8. Случайная величина X задана плотностью распределения

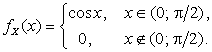
Найти математическое ожидание и дисперсию функции .

Решение. Найдем вначале математическое ожидание:

.

Вычислим теперь дисперсию:

.

Ответ: , .

Замечание. Математическое ожидание и дисперсию функции  можно было вычислить, найдя предварительно плотность распределения случайной величины Y.

 

Упражнения

2.3.1. Закон распределения случайной величины X имеет вид:

Найти закон распределения случайной величины .

2.3.2. Число X неисправностей на участке высоковольтной линии в течение года имеет распределение Пуассона с параметром a (). Общий материальный ущерб Y от этих неисправностей пропорционален квадрату их числа: , где  – неслучайная величина. Найти закон распределения этого ущерба.

2.3.3. СВДТ X имеет пуассоновское распределение , а . Вычислить .

2.3.4. Задана плотность распределения  случайной величины X, возможные значения которой заключены в интервале . Найти плотность распределения  случайной величины Y, если:

1) ; 2) ; 3) .

2.3.5. Задана плотность распределения  случайной величины X, возможные значения которой заключены в интервале . Найти плотность распределения  случайной величины Y, если:

1) ; 2) ; 3) .

 

Ответы к упражнениям

2.3.1.

2.3.2.

2.3.3. 1.

2.3.4. 1) 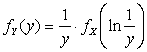, ; 2) , ; 3) , .

2.3.5. 1) , ;

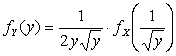2) , ; 3) , .

 

2.3.3. Функции многомерных случайных величин

 

Функция многомерной случайной величины определяется аналогично тому, как определялась функция одномерной случайной величины. Рассмотрим это на примере двумерной случайной величины. Пусть на вероятностном пространстве (, F, P) задана двумерная случайная величина . Предположим, что имеется числовая функция  скалярных аргументов x и y. Случайную величину  назовем функцией от двумерной случайной величины .

1. Пусть случайные величины X и Y являются дискретными.

Функция  от двумерной дискретной случайной величины  снова является дискретной случайной величиной, принимающей значения  с вероятностями , где  – множество возможных значений компоненты X,  – множество возможных значений компоненты Y. Тогда для нахождения функции распределения можно воспользоваться соотношением

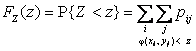
Однако, как правило, удобнее вначале составить ряд распределения случайной величины . Чтобы его построить, необходимо исключить все те значения , вероятность которых равна нулю, и объединить в один столбец все одинаковые значения , приписав этому столбцу суммарную вероятность.

 

Пример 2.3.9. Распределение случайного вектора  задано таблицей:

Составить закон распределения случайной величины .

Решение. Найдем вначале значения функции :

, , , , , .

Значит, случайная величина Z имеет два возможных значения:

, .

Вероятность возможного значения  равна сумме вероятностей несовместных событий  и , т.е. . Вероятность возможного значения  равна сумме вероятностей несовместных событий , ,  и , т.е. . Поэтому ряд распределения случайной величины Z имеет вид:

Таким образом, случайной величины Z имеет биномиальное распределение .

Ответ: .

 

2. Пусть случайные величины X и Y являются непрерывными.

В случае, когда  – двумерная непрерывная случайная величина с плотностью , функция распределения случайной величины  определяется формулой

.

Область интегрирования здесь состоит из всех точек x и y, для которых . Найдя функцию распределения , далее можно дифференцированием по z (в тех точках, в которых  имеет производную по z) найти плотность  распределения случайной величины Z.

 

Пример 2.3.10. Случайная точка  распределена равномерно в квадрате Q со стороной 1 (рис. 2.3.1 а). Найти закон распределения площади Z прямоугольника со сторонами X и Y: .

Решение. Очевидно, что в данном случае случайные величины X и Y независимы (Советуем убедиться в этом самостоятельно!):

 

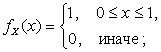
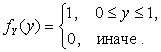
Область интегрирования  заштрихована на рис. 2.3.1 б.

                       

а                                                            б

Рис. 2.3.1.

Тогда

,

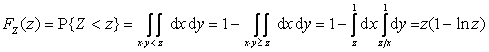где . Таким образом, окончательно получим:

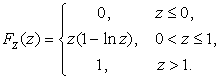
Дифференцируя это выражение по z, получим плотность распределения случайной величины Z:

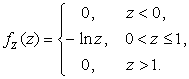
Ответ: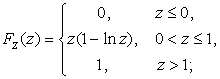  

 

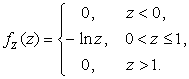
2.3.4. Задача композиции

Очень часто встречается функциональная зависимость вида

,

т.е. возникает задача определения закона распределения суммы компонент случайного вектора  по известному закону совместного распределения его компонент X и Y. Покажем, как эта задача решается в двух случаях, когда компоненты X и Y: 1) СВДТ; 2) СВНТ.

1.    Пусть X и Y – СВДТ с известным законом совместного распределения , где  – множество возможных значений компоненты X,  – множество возможных значений компоненты Y. Тогда закон распределения  записывается в виде

,

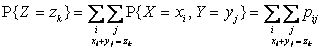где суммирование распространяется на все значения индексов i и j, для которых выполняется условие . Затем, построив ряд распределения случайной величины Z (исключая все те значения , вероятность которых равна нулю), можно составить функцию распределения .

Пример 2.3.11. Закон распределения случайного вектора  задан таблицей:

Составив закон распределения случайной величины , найти функцию распределения  и вычислить , .

Решение. Найдем вначале значения функции :

, , , , , .

Значит, случайная величина Z имеет пять возможных значений:

, , , , .

Вероятность возможного значения  равна сумме вероятностей несовместных событий  и , т.е. . Исключим значения  и , поскольку вероятности их равны нулю. Поэтому ряд распределения случайной величины Z имеет вид:

Тогда найдем функцию распределения :

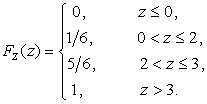
Вычислим теперь  и :

, .

Ответ:  , .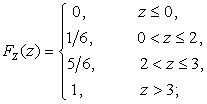

2.    Пусть X и Y – СВНТ с известной плотностью совместного распределения компонент , тогда

.

Особо важным для практики представляется частный случай, когда X и Y – независимые случайные величины, а . Получается так называемая задача композиции.

1.    Пусть X и Y – независимые СВДТ, тогда

или

.

Пример 2.3.12. Рассматривается случайная величина Z – суммарное число «успехов» в двух независимых опытах с одной и той же вероятностью «успеха» p в каждом опыте. Найти закон распределения случайной величины Z и составить ее функцию распределения.

Решение. Пусть X – количество успехов в первом опыте, а Y – количество успехов во втором опыте. По условию задачи X и Y независимы. Тогда . Получается задача композиции. Поскольку случайные величины X и Y принимают только два значения 0 или 1, то случайная величина  может принимать четыре значения

, , ,

с вероятностями

, qp, pq,

соответственно. Тогда ряд распределения примет вид

Составим теперь функцию распределения случайной величины :

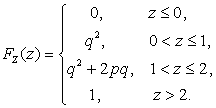
Ответ: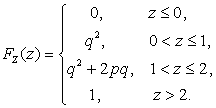

2.    Пусть X и Y – независимые СВНТ,  и  – их плотности. Плотность совместного распределения равна . Функция распределения суммы  равна

.

Этот интеграл можно вычислять как повторный:

Дифференцируя по z, получаем:

.

Две последние формулы носят название формул свертки. С помощью этих формул можно выразить функцию распределения  и плотность  суммы независимых случайных величин через плотности и функции распределения слагаемых. Отметим, что в силу симметрии переменных x и y формулы свертки можно записать следующим образом:

,

.

 

Пример 2.3.13. Пусть случайные величины X и Y – независимы,  – функция распределения Х, а Y имеет плотность

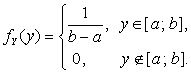
Составить функцию распределения и функцию плотности суммы .

Решение. Применяя формулу свертки, имеем

,

т.к. производная интеграла по переменной z равна значению подынтегральной функции от верхнего предела, умноженного на производную по z от верхнего предела, минус значение подынтегральной функции от нижнего предела, умноженного на производную по z от нижнего предела. Отсюда следует существование плотности

.

Ответ: , .

 

Пример 2.3.14. Случайные величины X и Y независимы и равномерно распределены на отрезке : , . Найти плотность вероятности случайной величины .

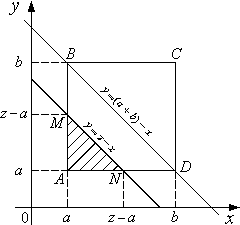
Решение. 1 способ. По условию возможные значения X определяются неравенством , возможные значения Y – неравенством . Отсюда следует, что возможные случайные точки  расположены в квадрате ABCD.

           

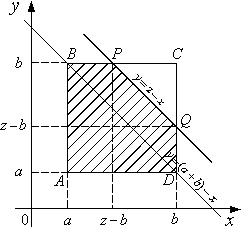
а                                                                  б

Рис. 2.3.2.

По определению функции распределения

.

Неравенству  удовлетворяют те точки  плоскости xOy, которые лежат ниже прямой  (эта прямая отсекает на осях Ox и Oy отрезки, равные z). Если же брать только возможные значения x и y, то неравенство  выполняется только для точек, лежащих в квадрате ABCD ниже прямой .

С другой стороны, т.к. случайные величины X и Y независимы, то

,

где область G – часть квадрата ABCD, которая расположена ниже прямой , а  – площадь G. Очевидно, что величина площади  зависит от значения z.

Если , то , поэтому . Если  (рис. 2.3.2 а), то , поэтому .

Если  (рис. 2.3.2 б), то

,

поэтому .

Если , , поэтому .

Найдем теперь плотность распределения , продифференцировав  по z:

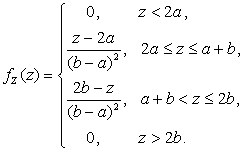
График функции плотности  так называемого треугольного распределения, или распределения Симпсона, показан на рис. 2.3.3.

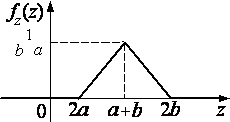
Рис. 2.3.3.

2 способ. Учтем, что в данном случае подынтегральное выражение в формуле свертки  отлично от нуля лишь в случае, когда  принадлежит отрезку , а именно:

, если ; , если .

Рассматривая два случая взаимного расположения отрезков, на которых плотности одновременно отличны от нуля (рис. 2.3.4), получим:

, если ;

, если .

Рис. 2.3.4.

Ответ: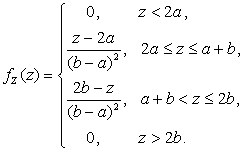

Определение. Закон распределения W определенного вида называется композиционно устойчивым, если из того, что две независимые случайные величины X и Y подчиняются закону распределения данного типа, следует, что их сумма  подчиняется закону распределения W того же вида (различаются только параметры этого закона).

Рассмотрим примеры композиционно устойчивых распределений.

 

Пример 2.3.15. Найти закон распределения суммы двух независимых случайных величин X и Y, распределенных по закону Пуассона: , .

Решение. Найдем вероятность события , где :

.

Следовательно, случайная величина  распределена по закону Пуассона с параметром . Значит, распределение Пуассона композиционно устойчиво.

Ответ: .

 

Пример 2.3.16. Найти закон распределения суммы двух независимых случайных величин X и Y, распределенных по биномиальному закону: , .

Решение. Представим случайную величину X в виде:

,

где  () – индикатор события A в i-м опыте:

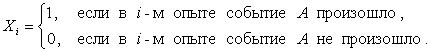
Ряд распределения случайной величины  имеет вид:

Аналогичное представление сделаем и для случайной величины Y:

,

где  () – индикатор события A в j-м опыте:

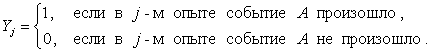
Ряд распределения случайной величины  имеет вид:

Следовательно,

,

где каждое из слагаемых является индикаторной случайной величиной распределенной по одному и тому же закону:

Всего слагаемых – . Отсюда следует, что случайная величина  распределена по биномиальному закону с параметрами ; p. Значит, биномиальное распределение композиционно устойчиво.

Ответ: .

Замечание 1. Если вероятности p в различных сериях опытов (первая серия опытов описывается случайной величиной X, а вторая серия – случайной величиной Y) будут различны, то в результате сложения двух независимых случайных величин X и Y, распределенных по биномиальным законам, получится случайная величина Z, распределенная не по биномиальному закону.

Замечание 2. Примеры 2.3.15 и 2.3.16 легко обобщаются на произвольное число слагаемых (Проделайте выкладки самостоятельно!).

 

Пример 2.3.17. Случайные величины X и Y независимы и нормально распределены: , . Найти плотность вероятности случайной величины .

Решение. Пользуясь формулой свертки , получим:

.

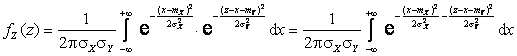Из курса интегрального исчисления известно, что

.

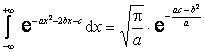В данном случае , , .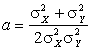

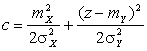Таким образом, из структуры плотности следует, что случайная величина  имеет нормальное распределение , где , . Значит, нормальное распределение композиционно устойчиво.

Ответ: , где , .

 

Упражнения

2.3.6. Независимые случайные величины имеют биномиальное распределение , . Вычислить значение , если .

2.3.7. Законы распределения случайных величин X и Y имеют вид:

Найти распределение случайной величины .

2.3.8. Законы распределения случайных величин X и Y имеют вид:

Найти распределение случайной величины .

2.3.9. Независимые случайные величины имеют показательное распределение , . Найти плотность распределения случайной величины .

2.3.10. Независимые случайные величины имеют равномерное распределение , . Найти функцию распределения и плотность распределения случайной величины .

2.3.11. Независимые случайные величины имеют равномерное распределение , . Найти функцию распределения и плотность распределения случайной величины .

2.3.12. Случайные величины X и Y независимы и нормально распределены: , . Найти плотность вероятности случайной величины .

 

Ответы к упражнениям

2.3.6. 0,84.

2.3.7.

2.3.8.

2.3.9.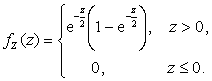 

2.3.10.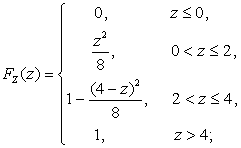 

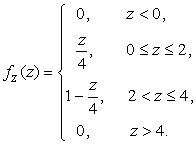
2.3.11.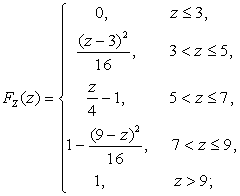 

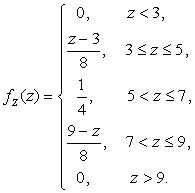
2.3.12. 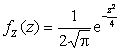, т.е. .

 

2.3.5. Числовые характеристики функций многомерных случайных величин

Сформулированные в пункте 2.3.2 правила нахождения числовых характеристик функций одномерных случайных величин естественным образом обобщаются на случай функций от бóльшего числа переменных. В частности, если  – двумерный случайный вектор с известным законом распределения и , где  – числовая функция скалярных аргументов x и y, то математическое ожидание и дисперсия случайной величины Z (если они существуют) могут быть найдены по следующим формулам:

,

если компоненты X и Y вектора  являются СВДТ,

,

если компоненты X и Y вектора  являются СВНТ;

,

если компоненты X и Y вектора  являются СВДТ,

,

если компоненты X и Y вектора  являются СВНТ.

Аналогичные формулы имеют место и для всех прочих начальных и центральных моментов распределения случайной величины .

Замечание. Таким образом, для вычисления числовых характеристик функции многомерной случайной величины  необязательно знать закон распределения случайной величины Z, а достаточно знать закон распределения случайного вектора .

 

Пример 2.3.18. Закон распределения случайного вектора  задан таблицей:

Не составляя закона распределения случайной величины , вычислить , .

Решение. Найдем вначале математическое ожидание:

.

Вычислим теперь дисперсию:

.

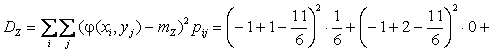
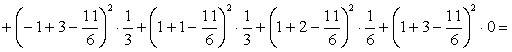
Сравните найденные числовые характеристики случайной величины  с аналогичными, полученными в примере 2.3.11.

Ответ: , .

 

В пункте 2.2.7 рассматривались условные числовые характеристики случайных векторов. В частности, определялись условные математические ожидания двумерных случайных векторов . Напомним, что если случайные величины X и Y дискретны, то условные математические ожидания вычисляются по формулам:

, .

Если случайные величины X и Y непрерывны, то условные математические ожидания вычисляются по формулам:

, .

Аналогично определяется условное математическое ожидание функции  при условии, что случайная величина Y приняла определенное значение (соответственно  при условии, что случайная величина X приняла определенное значение):

, ,

если случайные величины X и Y дискретны;

, ,

если случайные величины X и Y непрерывны.

Также имеют место следующие формулы полного математического ожидания:

, ,

если случайные величины X и Y дискретны;

, ,

если случайные величины X и Y непрерывны.

 

Пример 2.3.19. Число N радиотехнических приборов, сдаваемых покупателями в гарантийную мастерскую в течение дня, можно представить в виде случайной величины, хорошо описываемой распределением Пуассона , где a является средним числом приборов, сданных за день. Вероятность того, что сданный прибор потребует длительного ремонта, равна p. Найти среднее число приборов, требующих длительного ремонта.

Решение. При фиксированном числе n поступивших приборов количество приборов, требующих капитального ремонта, представляет собой случайную величину X с биномиальным распределением . Поэтому , . Поскольку случайная величина N имеет распределение Пуассона , то . Тогда по формуле полного математического ожидания

.

Ответ: .

 

2.3.6. Свойства математического ожидания и дисперсии

 

Если существуют соответствующие моменты, то справедливы следующие свойства математического ожидания и дисперсии:

1.    , где  – индикатор события А.

2.    Для любых случайных величин X и Y:

(аддитивное свойство математического ожидания).

Замечание. Для любых случайных величин  из свойства 2 по индукции выводится:

.

3.    Для любой константы c:

, .

4.    Для любых случайных величин X и Y: если , то .

В частности, если , то .

5.    Для любой случайной величины X: если  и , то .

6.    Для любой случайной величины X:

.

7.    Для любой случайной величины X:

(свойство неотрицательности дисперсии).

8.    Для любой константы c:

, .

9.    Для любых случайных величин X и Y:

 (или ).

В частности, если случайные величины X и Y некоррелированны, то

(мультипликативное свойство математического ожидания).

Замечание. Отметим, что для случайных величин , где , для выполнения свойства

недостаточно условия некоррелированности . Однако если случайные величины независимы, то последнее равенство верно.

10.  Для любых случайных величин X и Y:

.

Замечание. Для любых случайных величин  из свойства 11 по индукции выводится:

.

В частности, если случайные величины X и Y некоррелированны, то

(аддитивное свойство дисперсии).

Замечание. Если случайные величины  некоррелированны, то

.

Отметим также, что поскольку из независимости случайных величин следует их некоррелированность, то свойство 10 выполняется и для независимых случайных величин.

 

Пример 2.3.20. Известно, что случайная величина имеет биномиальное распределение . Найти  и .

Решение. По свойству 8 математического ожидания и дисперсии . Поскольку для случайной величины  дисперсия , где по условию задачи , , , то

.

Вычислим теперь . Опираясь на свойства 2 и 3 математического ожидания и дисперсии, получим:

.

Поскольку для случайной величины  математическое ожидание  и, по свойству 6, , то

.

Ответ: , .

 

Пример 2.3.21. Функция распределения СВНТ X имеет вид:

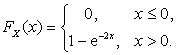
Найти  и .

Решение. По условию задачи случайная величина X распределена по экспоненциальному закону: . Поэтому , . Найдем вначале : . Тогда:

.

По свойству 8 математического ожидания и дисперсии:

.

Ответ: , .

Пример 2.3.22. Известно, что , , . Найти  и .

Решение. Используя формулу для дисперсии суммы

,

получим . Тогда

.

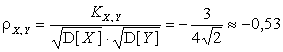Ответ: , .

 

Пример 2.3.23. На столе налогового инспектора лежат три декларации от представителей трех различных групп населения. Вероятности сокрытия доходов при заполнении декларации для одного представителя каждой группы равны соответственно 0,05, 0,1 и 0,15. Предположим, что сокрытие доходов обнаруживается при проверке в 100% случаев. Найти средний доход государства от проверки этих деклараций, если сумма налагаемого штрафа при обнаружении сокрытия дохода составляет по группам населения 100, 250 и 500 минимальных окладов соответственно.

Решение. Рассмотрим случайную величину X, равную доходу государства от проверки трех деклараций. Тогда X можно представить в виде

,

где  () индикаторные случайные величины, т.е. , если подавший декларацию представитель i-й группы населения скрывает доход, и  – в противном случае. По условию задачи требуется найти средний доход государства от проверки налоговых деклараций, т.е. математическое ожидание случайной величины X. Воспользуемся свойствами математического ожидания для вычисления :

.

Поскольку для индикаторных случайных величин  (), то

.

Ответ: средний доход государства от проверки поданных трех деклараций составит 105 минимальных окладов.

 

Пример 2.3.24. Известно, что случайные величины X и Y (где X – рост наугад взятого взрослого мужчины и Y – его вес) удовлетворительно описываются нормальным законом распределения: , . Ковариация этих признаков равна . Считается, что человек страдает избыточным весом, если выполняется неравенство . Найти математическое ожидание и дисперсию характеристики избыточного веса , а также вероятность того, что наугад выбранный мужчина страдает избыточным весом.

Решение. Так как случайные величины X и Y распределены нормально, то разность  также распределена нормально (Проверьте!). Вычислим параметры этого закона распределения:

; .

Таким образом,  и, следовательно,

.

Ответ: , , .

 

Упражнения

2.3.13. СВНТ X имеет плотность вероятности

.

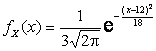Найти  и .

2.3.14. Плотность вероятности случайной величины X имеет следующий вид:

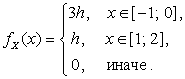
Найти  и .

2.3.15. Пусть существуют дисперсии случайных величин X и Y такие, что . Чему равна ковариация случайных величин  и ?

2.3.16. Известно, что случайная величина , , . Найти .

2.3.17. Известно, что случайная величина . Пусть . Найти .

2.3.18. Известно, что случайные величины , . Вычислить .

2.3.19. Подбрасывают три игральные кости. Рассматриваются случайные величины: X – количество костей, на которых выпало шесть очков, Y – количество костей, на которых выпало пять очков. Найти  и закон распределения случайной величины .

2.3.20. Предприятие имеет две поточные линии по сборке некоторой продукции. Технологические процессы на линиях связаны между собой. Рассматривая в качестве случайной величины X – количество единиц продукции, собранной за день на первой линии, а Y – на второй линии, совместное распределение этих величин можно задать с помощью таблицы:

Составить закон распределения случайной величины  – суммарного количества единиц продукции, выпускаемой предприятием за день. Найти  и .

 

Ответы к упражнениям

2.3.13. , .

2.3.14. , .

2.3.15. 0.

2.3.16. 0.

2.3.17. 0.

2.3.18. .

2.3.19. , .

2.3.20. , ; закон распределения Z:

 

2.3.7. Характеристическая функция

Если  – комплекснозначная случайная величина, где X и Y – действительные случайные величины, то

.

Определение. Характеристической функцией случайной величины X называется комплекснозначная функция

,

где , .

В частности,

, если X – СВДТ;

, если X – СВНТ.

Замечание 1. По характеристической функции  однозначно восстанавливается функция распределения .

Замечание 2. Характеристическая функция представляет собой преобразование Фурье плотности вероятности  СВНТ X. Поэтому обратное преобразование Фурье приводит к соотношению

.

Таким образом, для СВНТ задание  равносильно заданию , и наоборот.

Характеристическая функция  обладает следующими свойствами:

1.    .

2.    .

3.    Если существует m-й абсолютный момент , то существуют производные характеристической функции  до m-го порядка включительно, причем 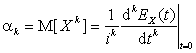, где .

4.    Если , то .

5.    Если , причем  независимы в совокупности, то .

Замечание. Пользуясь этим свойством, можно решать задачу определения закона распределения суммы независимых случайных величин (задачи композиции). Действительно, если , то . Найдя , можно по характеристической функции восстановить закон распределения случайной величины Z. Кроме того, по виду  можно ответить на вопрос о композиционной устойчивости распределения.

6.    , где черта означает операцию комплексного сопряжения. В частности, отсюда следует, что если  – действительная функция, то она обязательно четная.

Определение. Характеристической функцией случайного вектора  называется комплекснозначная функция n действительных переменных , определяемая равенством

.

 

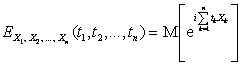Пример 2.3.25. Найти характеристическую функцию случайной величины X, имеющей биномиальное распределение (), и с ее помощью вычислить ,  и .

Решение. Согласно определению характеристической функции СВДТ X

.

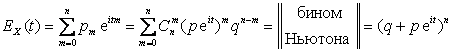По свойству 3 для :

,

.

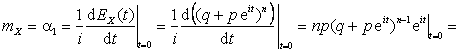
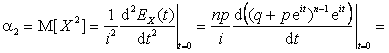
Отсюда

, .

 

Пример 2.3.26. Найти характеристическую функцию случайной величины X, имеющей пуассоновское распределение (), и с ее помощью вычислить ,  и .

Решение. Согласно определению характеристической функции СВДТ X

.

По свойству 3 для :

,

.

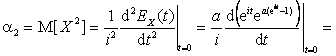
Отсюда

, .

 

Пример 2.3.27. Найти характеристическую функцию случайной величины X, имеющей геометрическое распределение (), и с ее помощью вычислить ,  и .

Решение. Согласно определению характеристической функции СВДТ X

.

По свойству 3 для :

,

.

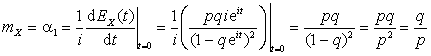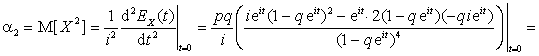
Отсюда

, .

 

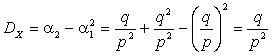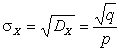Пример 2.3.28. Найти характеристическую функцию случайной величины X, имеющей равномерное распределение ().

Решение. Согласно определению характеристической функции СВНТ X

.

Замечание. Для случайной величины  с помощью характеристической функции можно вычислить ,  и . Однако это не очень удобно, поэтому мы этого не делаем.

 

Пример 2.3.29. Найти характеристическую функцию случайной величины X, имеющей показательное распределение (), и с ее помощью вычислить ,  и .

Решение. Согласно определению характеристической функции СВНТ X

.

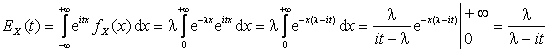По свойству 3 для :

,

,

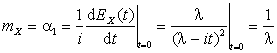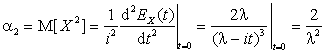Отсюда

, .

 

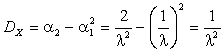Пример 2.3.30. Найти характеристическую функцию случайной величины X, имеющей нормальное распределение (), и с ее помощью вычислить ,  и .

Решение. Найдем вначале характеристическую функцию случайной величины . Согласно определению характеристической функции СВНТ X

Дифференцируя  (по t) и применяя метод интегрирования по частям, получим:

.

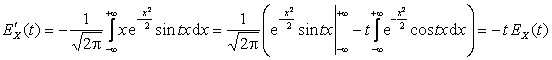Решая это дифференциальное уравнение с разделяющимися переменными при начальном условии  (свойство 2 характеристической функции), находим . Отсюда характеристическая функция случайной величины  имеет вид

.

Рассмотрим теперь случайную величину . Тогда нормированная случайная величина  имеет нормальное распределение  и, следовательно, характеристическую функцию . Далее, по свойству 4 характеристической функции, для случайной величины  имеем

.

Найдем теперь математическое ожидание, дисперсию и среднее квадратическое отклонение :

,

,

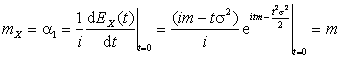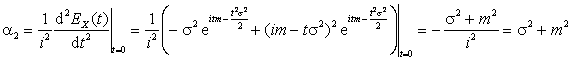Отсюда

, .

Пример 2.3.31. Проверить композиционную устойчивость нормального закона.

Решение. Пусть независимые случайные величины X и Y имеют нормальное распределение: , . Найдем  случайной величины , учитывая свойство 5 характеристической функции и опираясь на результаты примера 2.3.30:

.

Откуда видно, что характеристическая функция  соответствует нормальному распределению, причем . Значит, нормальный закон является композиционно устойчивым.

 

Упражнения

2.3.21. Задана характеристическая функция СВНТ X:

.

Найти плотность  распределения случайной величины X.

2.3.22. Случайные величины X и Y независимы и распределены по закону Пуассона: , . С помощью характеристической функции доказать композиционную устойчивость закона Пуассона.

2.3.23. Случайные величины X и Y независимы и распределены по биномиальному закону: , . С помощью характеристической функции доказать композиционную устойчивость биномиального закона.

2.3.24. Случайные величины X и Y независимы и распределены по одному закону . Является ли закон  композиционно устойчивым?

 

 

Ответы к упражнениям

2.3.21.  – распределение Коши.

2.3.24. Нет.