2.2. Случайные векторы

Пусть на одном и том же вероятностном пространстве (, F, P) задано n случайных величин , , …, . Совокупность случайных величин  называется многомерной (n-мерной) случайной величиной, или (n-мерным) случайным вектором.

Пример 2.2.1. Широта X и долгота Y падения метеорита на Землю представляют собой двумерный случайный вектор . В эту модель можно ввести также третью координату Z – время от начала наблюдений до момента падения первого метеорита на Землю. Тогда получится трехмерный случайный вектор .

Пример 2.2.2. Успеваемость студента, окончившего курс обучения в вузе, характеризуется системой n случайных величин  – оценками, проставленными в его дипломе.

 

2.2.1. Совместная функция распределения

 

Рассмотрим на одном и том же вероятностном пространстве (, F, P) несколько случайных величин . Так как множества , т.е. являются событиями, то и их пересечение . Поэтому существует вероятность этого события.

Определение. Многомерной функцией распределения  называется вероятность события :

.

В дальнейшем изложении ограничимся случаем двух случайных величин . Поэтому будем рассматривать .

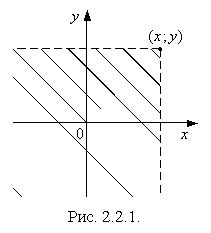Замечание 1. Геометрически значение  – это вероятность попадания случайной точки  в бесконечный квадрант с вершиной  (на рис. 2.2.1 этот квадрант показан штриховкой).

Замечание 2. С помощью , можно вычислять вероятности попадания случайной точки в полуполосу или в прямоугольник:

а)  (рис. 2.2.2 а);

б)  (рис. 2.2.2 б);

в)

 (рис. 2.2.2 в);

 

        

                 а                                     б                                                в

Рис. 2.2.2.

Пример 2.2.3. Дана двумерная функция распределения: , где , . Найти вероятность попадания случайной точки  в прямоугольник, ограниченный прямыми , , , .

Решение. 

.

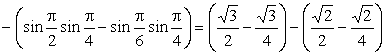
Ответ: .

Из формулы вычисления вероятности попадания в прямоугольник и определения многомерной функции распределения , вытекают ее свойства, которые доказываются аналогично одномерному случаю:

1.    по каждому аргументу не убывает и непрерывна слева.

2.    .

3.    .

4.    а) При  двумерная функция распределения  становится функцией распределения компоненты X: .

б) При  двумерная функция распределения  становится функцией распределения компоненты Y: .

 

2.2.2. Дискретные двумерные случайные величины

 

Определение. Двумерная случайная величина  называется дискретной, если случайные величины Х и Y дискретны.

Если случайная величина Х может принимать только значения  (для простоты изложения ограничимся только конечным множеством значений), а случайная величина Y – значения , то двумерный случайный вектор  может принимать только пары значений , где , . Также, как и в одномерном случае, распределение двумерной дискретной случайной величины естественно описывается с помощью таблицы:

В этой таблице  и .

Одномерные законы распределения отдельных компонент случайного вектора  выражаются через вероятности совместных значений  по формулам:

, ,

где суммирование распространяется на все возможные значения индексов i или j. Уточним, что для получения значения вероятности  для некоторого фиксированного значения i, надо сложить вероятности , стоящие в i-ой строке таблицы, а для получения значения вероятности  для некоторого фиксированного значения j, надо сложить вероятности , стоящие в j-ом столбце таблицы. При этом удобно одномерные законы распределения отдельных компонент записывать в той же таблице (см. ее последнюю строку и последний столбец). В правом нижнем углу таблицы обязательно должна находиться единица, являющаяся результатом суммирования вероятностей в ее последней строке (последнем столбце) и соответствующая условию нормировки. С помощью таблицы нетрудно определить функцию распределения

.

Также легко по таблице вычисляется вероятность любого события B, задаваемого в виде произвольной области на плоскости:

.

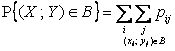Пример 2.2.4. Закон распределения двумерного дискретного случайного вектора  задан таблицей:

Найти: одномерные законы распределения компонент X и Y; вероятность . Составить функцию распределения .

Решение. 1) Одномерные законы  и  распределения компонент X и Y соответственно построены в таблице:

 

2) .

3) Согласно определению функции распределения . Напомним, что геометрически значение  – это вероятность попадания случайной точки  в бесконечный квадрант с вершиной . Для вершины этого квадранта, согласно условию задачи, есть двенадцать областей, образованных тремя вертикальными прямыми , ,  и двумя горизонтальными прямыми , .

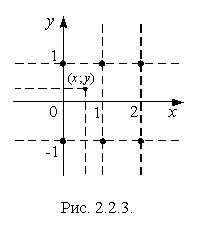На рис. 2.2.3 показан случай, когда вершина  находится внутри прямоугольника , . При этом внутри квадранта находится только одна точка с координатами , в которой имеется ненулевая вероятность, равная 0,1. Функцию распределения  удобно задавать в виде таблицы (ее значение для случая, когда вершина  квадранта находится внутри прямоугольника ,  выделено жирным шрифтом):

 

 

 

Пример 2.2.5. Известна функция распределения  двумерного дискретного случайного вектора :

 

 

 

Составить функции распределения  и  компонент X и Y, а затем построить их законы распределения.

Решение. Учитывая, что , , получим («проходя» соответственно по последнему столбцу и последней строке таблицы):

  

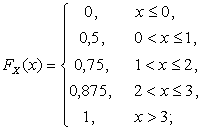
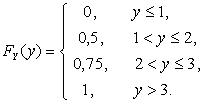
Значит, для случайной величины X функция распределения испытывает «скачки» в точках , для случайной величины Y – в точках . Поэтому законы распределения компонент выглядят следующим образом:

 

2.2.3. Непрерывные двумерные случайные величины

Определение. Неотрицательная кусочно-непрерывная функция  называется плотностью распределения (плотностью вероятности) двумерной случайной величины , если

,

где использована символическая запись для двойного интеграла по области . Такая двумерная случайная величина  называется непрерывной.

Функция плотности  обладает следующими свойствами:

1.    для всех .

2. 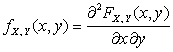   во всех точках непрерывности функции .

3.    (условие нормировки).

4. 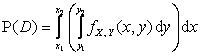   , где  – прямоугольник на плоскости .

5.    , где D – произвольная квадрируемая область на плоскости .

6. 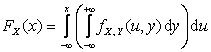   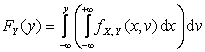, , где ,  – функции распределения компонент X и Y.

7.    , , где ,  – функции плотности распределения компонент X и Y.

Пример 2.2.6. Известна функция плотности двумерного случайного вектора :

, .

Составить функцию распределения .

Решение. По определению функции распределения

,

поэтому:

.

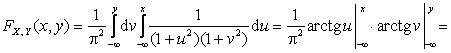
Ответ: .

Пример 2.2.7. Найти плотность распределения двумерного случайного вектора , если известна функция распределения

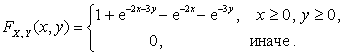
Решение. Согласно свойству 2 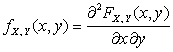 во всех точках непрерывности функции . Поэтому

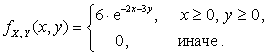
Ответ: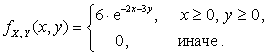

Пример 2.2.8 (двумерное равномерное распределение). Плотность  равномерного распределения на области  конечной двумерной площади :

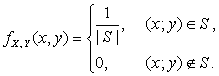
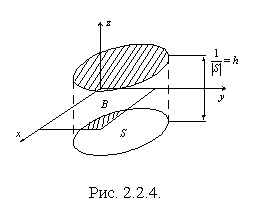Вероятность  в этом случае определяется отношением площадей  и S (рис. 2.2.4):

.

Замечание. По последней формуле вычисляются так называемые геометрические вероятности.

Пример 2.2.9. Двумерный случайный вектор  подчинен закону распределения с плотностью

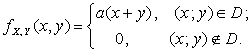
Область D – треугольник, ограниченный прямыми , , . Найти коэффициент а.

Решение. Согласно условию нормировки . Поскольку только в области D подынтегральная функция  отлична от нуля, то имеем уравнение

, или .

Тогда

.

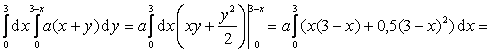
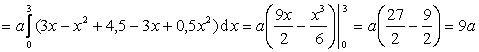Отсюда, решая уравнение , получим .

Ответ: .

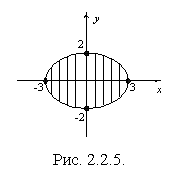Пример 2.2.10. Известна функция плотности двумерного случайного вектора  (рис. 2.2.5):

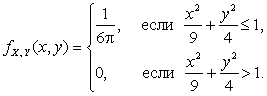
Найти плотности распределения  и  компонент X и Y.

Решение. Очевидно, что если , то . Пусть , тогда:

.

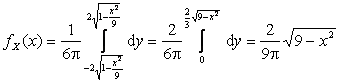Итак,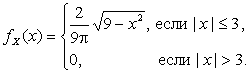

Аналогично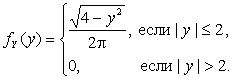

Ответ: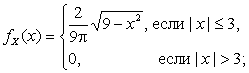  

 

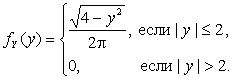
Упражнения

2.2.1. Найти вероятность того, что случайно брошенная точка с координатами  попадет на область D, определенную неравенствами , если функция распределения координат этой точки равна

2.2.2. Пусть  – функция распределения случайного вектора . Будет ли  функцией распределения некоторой случайной величины? Ответ необходимо обосновать.

2.2.3. Является ли функция , где , функцией распределения некоторого случайного вектора ?

2.2.4. Закон распределения двумерного дискретного случайного вектора  задан таблицей:

Найти: 1) одномерные законы распределения компонент X и Y; 2) вероятность . 3) Составить функцию распределения .

2.2.5. Закон распределения двумерного дискретного случайного вектора  задан таблицей:

Найти: 1) одномерные законы распределения компонент X и Y; 2) вероятность . Составить функцию распределения .

2.2.6. Монета бросается до первого выпадения герба, но не более 3 раз. Случайная величина Х – число выпадений решки, Y – число подбрасываний. Описать закон распределения случайного вектора . Найти одномерные законы распределения компонент X и Y. Вычислить вероятность .

2.2.7. Стрелок 3 раза стреляет по мишени с вероятностью 0,7 попадания при каждом выстреле. Случайная величина Х – модуль разности между числом попаданий и числом промахов, Y – число попаданий. Описать закон распределения случайного вектора . Найти одномерные законы распределения компонент X и Y. Вычислить вероятность .

2.2.8. Система случайных величин  подчинена закону распределения с плотностью

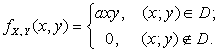
Область D – квадрат, ограниченный прямыми , , , . Найти коэффициент а.

2.2.9. Случайный вектор  имеет плотность распределения

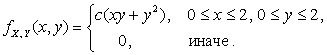
Найти: 1) постоянную c; 2) вероятность ; 3) плотности распределения компонент X и Y; 4) функции распределения компонент X и Y.

2.2.10. Случайный вектор  имеет функцию распределения

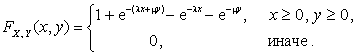
Найти законы распределения компонент X и Y.

2.2.11. Случайный вектор  имеет функцию распределения

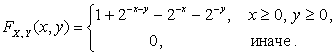
Найти: 1) двумерную плотность распределения случайного вектора ;

2) вероятность попадания случайной точки с координатами  в треугольник с вершинами , , .

 

Ответы к упражнениям

2.2.1. .

2.2.2. Нет. Указание. Рассмотреть, например, функцию распределения  упражнения 2.2.1.

2.2.3. Нет.

2.2.4.

; функция распределения :

 

2.2.5.

; функция распределения :

 

2.2.6. ;

2.2.7. ;

2.2.8. .

2.2.9. 1) ; 2) ;

3) 

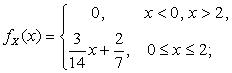
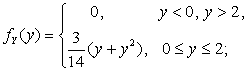
4) 

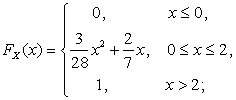
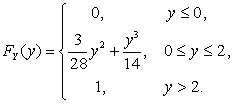
2.2.10. , .

2.2.11. 1) 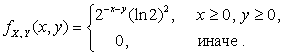 2) .

 

 

2.2.4. Зависимые и независимые случайные величины

 

В двух предыдущих пунктах было показано, как, зная закон распределения системы двух (дискретных или непрерывных) случайных величин, найти законы распределения отдельных компонент X и Y.

Вопрос: «Можно ли, зная законы распределения отдельных случайных величин X и Y, входящих в систему, найти закон распределения всей системы?»

Прежде, чем ответить на этот вопрос, рассмотрим пример.

Пример 2.2.11. Законы распределений СВДТ X и Y заданы при помощи таблиц:

Построим следующие две таблицы:

Распределения соответствующих компонент в одной и другой таблицах одинаковы. Однако очевидно, что эти таблицы описывают абсолютно различные распределения двумерного случайного вектора  (все значения  в одной таблице отличны от соответствующих значений  в другой таблице).

Таким образом, на поставленный выше вопрос можно дать следующий ответ: «Зная законы распределения отдельных случайных величин X и Y, входящих в систему, найти закон распределения всей системы в общем случае нельзя».

Заметим, что это можно сделать только в одном частном случае, когда случайные величины X и Y, образующие систему, независимы.

Определение. Две случайные величины X и Y называются независимыми, если независимы все связанные с ними события.

Например,  и ;  и  и т.д.

Замечание. Так как зависимость и независимость событий всегда взаимны (если событие A не зависит от события B, то и событие B не зависит от события A), поэтому зависимость и независимость случайных величин также всегда взаимны: если случайная величина X не зависит от случайной величины Y, то Y не зависит от X.

В терминах законов распределения независимость случайных величин можно определить так: «Две случайные величины называются независимыми, если закон распределения каждой из них не зависит от того, какое значение приняла другая».

Если компоненты X и Y двумерного вектора  независимы, то функция распределения  выражается, через функции распределения отдельных компонент:

.

Верно и обратное утверждение. Это правило является необходимым и достаточным условием независимости для случайных величин любого типа.

Необходимые и достаточные условия независимости компонент X и Y для дискретного и непрерывного случаев:

1.    X и Y являются независимыми дискретными случайными величинами тогда и только тогда, когда для всех значений индексов i и j выполняется

.

2.    X и Y являются независимыми непрерывными случайными величинами тогда и только тогда, когда

.

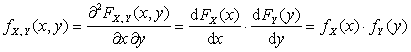Отметим, что допускается нарушение последнего равенства на множестве точек , имеющих двумерную площадь, равную нулю.

Пример 2.2.12. Закон распределения двумерного дискретного случайного вектора  задан таблицей:

 

Определить, зависимы или независимы компоненты X и Y.

Решение. Составим законы распределения компонент X и Y:

Проверим теперь выполнение условия  для всех пар индексов , . Очевидно, что это условие выполнено для любых i и j. Значит, компоненты X и Y независимы.

Ответ: компоненты X и Y независимы.

Замечание. В данном случае независимость компонент X и Y можно было установить, внимательно посмотрев на исходную таблицу, задающую закон распределения случайного вектора . Из этой таблицы видно, что закон распределения каждой из компонент не зависит от того, какое значение приняла другая компонента.

Пример 2.2.13. Система двух непрерывных случайных величин  имеет плотность распределения

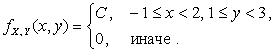
Найти константу С. Определить, зависимы или независимы X и Y. Составить функцию распределения .

Решение. Из условия нормировки для функции плотности  имеем:

,

отсюда . Таким образом,

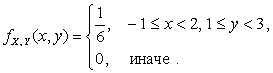
Найдем функции плотности отдельных компонент:

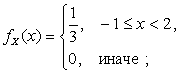
, т.е.

, т.е.

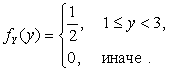
Очевидно, что равенство  выполняется для всех точек координатной плоскости. Значит, компоненты X и Y независимы. Найдем функцию распределения системы . Так как компоненты независимы, значит, . Найдем вначале  и :

  

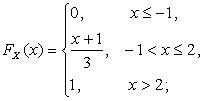
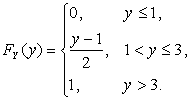
Перемножая  и  при «прямоугольнику» и учитывая, что , , получим:

 

2.2.5. Числовые характеристики двумерных случайных векторов.

 

Ковариация и коэффициент корреляции

Определение. Начальным моментом порядка  системы двух случайных величин  называется действительное число , определяемое по формуле:

,

если  – система двух дискретных случайных величин;

,

если  – система двух непрерывных случайных величин.

Определение. Центральным моментом порядка  системы двух случайных величин  называется действительное число , определяемое по формуле:

,

если  – система двух дискретных случайных величин;

,

если  – система двух непрерывных случайных величин.

На практике чаще всего встречаются моменты первого и второго порядков. Очевидно, что начальные моменты первого порядка есть не что иное, как математические ожидания компонент X и Y:

, .

Точка с координатами  на плоскости xOy представляет собой характеристику положения случайной точки , а ее рассеивание (разброс) происходит вокруг .

Центральные моменты первого порядка, очевидно, равны нулю, т.е.

.

Имеются три начальных момента второго порядка – ,  и . Причем первые два из них есть не что иное, как начальные моменты второго порядка компонент X и Y:

, .

Имеются три центральных момента второго порядка ,  и . Первые два из них представляют собой дисперсии компонент X и Y соответственно:

, .

Рассмотрим  отдельно.

Определение. Центральный момент второго порядка  называется ковариацией случайной величины .

Для момента  используется обозначение .

Замечание. По определению ковариации: .

В механической интерпретации, когда распределение вероятностей на плоскости xOy трактуется как распределение единичной массы на этой плоскости, точка  есть не что иное, как центр масс распределения; дисперсии  и  – моменты инерции распределения относительно точки  в направлении осей Ox и Oy соответственно, а ковариация – это центробежный момент инерции распределения масс.

Теорема. Если случайные величины X и Y независимы, то .

Замечание. Как правило,  удобнее вычислять по формуле

.

Ковариация  характеризует не только степень зависимости двух случайных величин , но также их рассеивание вокруг точки . Однако размерность ковариации  равна произведению размерностей случайных величин X и Y. Чтобы получить безразмерную величину, характеризующую только зависимость, а не разброс, ковариацию  делят на произведение :

.

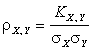Определение. Величина  называется коэффициентом корреляции случайных величин X и Y.

Коэффициент корреляции  характеризует степень зависимости случайных величин X и Y, причем не любой зависимости, а только линейной, проявляющейся в том, что при возрастании одной случайной величины другая проявляет тенденцию также возрастать (или убывать). В первом случае  и говорят, что случайные величины X и Y связаны положительной корреляцией, во втором случае  и говорят, что случайные величины X и Y связаны отрицательной корреляцией. Модуль коэффициента корреляции случайных величин X и Y характеризует степень тесноты линейной зависимости между ними. Если линейной зависимости нет, то .

Теорема. Если случайные величины X и Y связывает линейная зависимость , то  при ,  при .

Пример 2.2.14. Найти коэффициент корреляции  между случайными величинами: 1) X и ; 2) X и .

Решение. Согласно теореме 3.5.2: 1) , т.к. , ; 2) , т.к. , .

Ответ: 1) ; 2) .

Пример 2.2.15. Игральная кость размечена таким образом, что сумма очков на противоположных гранях равна 7 (т.е. 1 и 6, 2 и 5, 3 и 4). Пусть X – число очков на верхней грани, Y – число очков на нижней грани. Построить совместный закон распределения случайных величин X и Y, найти коэффициент корреляции между ними.

Решение. По условию задачи . Поэтому . Следовательно, для построения таблицы распределения случайного вектора  остается вычислить вероятности:

,

.

Аналогично можно показать, что

, .

Тогда закон распределения случайного вектора  задается следующей таблицей:

 

 

 

 

Поскольку между случайными величинами X и Y имеется линейная связь , то .

Ответ: .

Теорема. Для любых случайных величин X и Y:

.

Определение. Случайные величины X и Y называются некоррелированными, если  (или ), иначе X и Y называются коррелированными.

Замечание. Из независимости случайных величин следует их некоррелированность. Но из некоррелированности () не вытекает их независимость. Действительно, если , то это означает только отсутствие линейной связи между случайными величинами, однако любой другой вид связи может при этом присутствовать.

Пример 2.2.16. Закон распределения случайного вектора  задан таблицей:

 

Выяснить, зависимы или нет случайные величины X и Y. Найти: .

Решение. Найдем законы распределения компонент X и Y:

Очевидно, что компоненты X и Y являются зависимыми, т.к.

.

; ;

, ;

, ;

;

.

Так как , то это показывает, что между случайными величинами X и Y существует отрицательная линейная зависимость, т.е. при увеличении одной из них другая имеет тенденцию уменьшаться.

Пример 2.2.17. Закон распределения случайного вектора  задан таблицей:

 

Выяснить, являются ли случайные величины X и Y: 1) зависимыми; 2) коррелированными.

Решение. Найдем законы распределения компонент X и Y:

Очевидно, что компоненты X и Y являются зависимыми, т.к.

.

; ;

, ;

, ;

; .

Этот пример показывает, что случайные величины X и Y могут быть некоррелированными, но при этом являться зависимыми.

Пример 2.2.18. Двумерный случайный вектор  подчинен закону распределения с плотностью

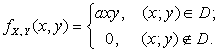
Область D – треугольник, ограниченный прямыми , , .

Найти: коэффициент а, . Выяснить, зависимы или нет случайные величины X и Y.

Решение. Коэффициент a находится из уравнения

.

Опуская промежуточные выкладки (в этом примере будем делать так и в дальнейшем), получаем . Далее:

,

.

Заметим, что в силу симметрии по переменным x и y, можно не вычислять математическое ожидание и дисперсию компоненты Y, т.е. , . Тогда .

Вычислим ковариацию и коэффициент корреляции:

; .

Поскольку компоненты X и Y коррелированны, следовательно, они зависимы.

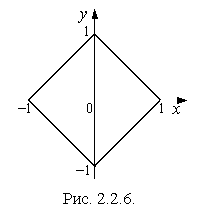Ответ: , , , , , . Компоненты X и Y зависимы.

Пример 2.2.19. Двумерный случайный вектор  равномерно распределен на множестве случайных точек Q, задаваемых неравенством . Выяснить, являются ли случайные величины X и Y: 1) зависимыми; 2) коррелированными.

Решение. Множество точек Q, задаваемых неравенством , является квадратом (рис. 2.2.6). Поскольку двумерный случайный вектор  равномерно распределен на множестве Q, его плотность имеет вид

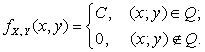
Из условия нормировки найдем константу C:

,

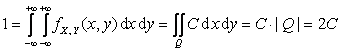где  – площадь квадрата Q, равная 2. Отсюда , а значит,

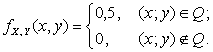
1) Найдем вначале плотность распределения компоненты X.

Если , то, очевидно,  для всех .

Если , то

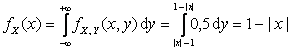, т.е.

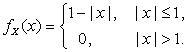
Аналогично находится плотность распределения компоненты Y:

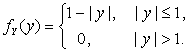
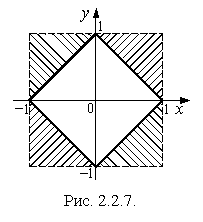
Равенство  не выполняется для точек координатной плоскости, принадлежащих заштрихованным областям (рис. 2.2.7), поскольку в этих точках , а  и . Суммарная площадь заштрихованных областей равна 2, значит, компоненты X и Y зависимы.

2) Вычислим математические ожидания компонент X и Y:

,

т.к. интеграл от нечетной функции в симметричных пределах равен нулю. Аналогично .

Определим начальный момент :

.

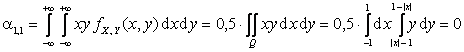Таким образом, ковариация . Значит, компоненты X и Y некоррелированные.

Ответ: компоненты X и Y зависимы, но некоррелированны.

 

Упражнения

2.2.12. Две независимые случайные величины X и Y подчинены показательному закону распределения: , . Написать выражение совместной плотности вероятности. Вычислить вероятность попадания случайной точки  в квадрат с вершинами , , , .

2.2.13. Случайные величины X и Y независимы, причем: , . 1) Написать выражение совместной плотности вероятности. 2) Составить функцию распределения случайного вектора . 3) Вычислить вероятность попадания случайной точки  в область .

2.2.14. Найти ковариацию , где X – некоторая случайная величина, а c – константа.

2.2.15. Известно, что следующие числовые характеристики некоторой случайной величины X: , . Найти ковариацию .

2.2.16. Вычислить коэффициент корреляции  и составить функцию распределения  двумерного дискретного случайного вектора, закон распределения которого задан таблицей:

2.2.17. Дважды бросается игральная кость. Случайная величина Х – число появлений «шестерки», случайная величина Y – число появлений нечетной цифры. Описать закон распределения случайного вектора . Найти центр рассеивания и коэффициент корреляции.

2.2.18. Число Х выбирается из множества целых чисел . Затем из этого же множества выбирается наудачу число Y, бóльшее или равное первому. Описать закон распределения случайного вектора . Найти центр рассеивания и коэффициент корреляции.

2.2.19. Двумерный случайный вектор  подчинен закону распределения с плотностью

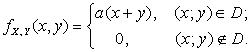
Область D – квадрат, ограниченный прямыми , , , .

Найти: коэффициент а, . Вычислить вероятность попадания случайной точки  в квадрат Q, ограниченный прямыми , , , .

2.2.20. В продукции завода брак вследствие дефекта A составляет 3%, а вследствие дефекта B – 4,5%. Годная продукция составляет 95%. Определить, какой процент всей продукции обладает дефектами обоих типов. Найти коэффициент корреляции дефектов A и B.

2.2.21. Брак в продукции завода вследствие дефекта A составил 6%, причем среди забракованной по признаку A продукции в 4% случаев встречается дефект B, а в продукции, свободной от дефекта A, дефект B встречается в 1% случаев. Найти вероятность встретить дефект B во всей продукции и коэффициент корреляции дефектов A и B.

2.2.22. Случайный вектор  подчинен закону распределения с плотностью

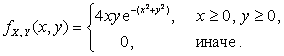
Найти коэффициент корреляции .

 

Ответы к упражнениям

2.2.12. 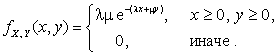, значение искомой вероятности равно .

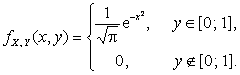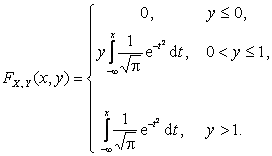2.2.13. 1)  2)  3) .

2.2.14. 0.

2.2.15. 1.

2.2.16.

, , , , ;

функция распределения :

 

2.2.17.

, , , , .

2.2.18.

, , , , .

2.2.19. , , , , , ; .

2.2.20. 2,5%; . Указание. Введите индикаторные случайные величины: X – индикатор брака вследствие дефекта A при испытании одной детали (, если деталь обладает дефектом A,  в противном случае), Y – индикатор брака вследствие дефекта B при испытании одной детали. Затем опишите закон распределения случайного вектора .

2.2.21. Вероятность встретить дефект B ; коэффициент корреляции .

2.2.22. .

 

2.2.6. Условные законы распределения

 

Если случайные величины, образующие систему, зависимы, то для нахождения закона распределения системы недостаточно знать законы распределения отдельных величин, входящих в систему. Требуется еще знать так называемый условный закон распределения одной из них.

Определение. Условным законом распределения одной из величин , входящих в систему, называется ее закон распределения, вычисленный при условии, что другая случайная величина приняла определенное значение.

Начнем с наиболее простого случая. Пусть случайная величина Y является дискретной.

Определение. Условной функцией распределения  случайной величины X при условии  называется условная вероятность события  при условии события , т.е.

.

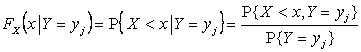Аналогично определяется условная функция распределения  случайной величины Y при условии  (когда случайная величина X является дискретной):

.

Замечание 1. Условная функция распределения обладает всеми свойствами, которые присущи обычной (безусловной) функции распределения.

Замечание 2. Если случайная величина X также дискретная, причем , то удобно рассматривать условную вероятность случайной величине X принять значение  при условии :

.

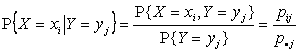Обычно условное распределение  описывают с помощью таблицы. Ясно, что элементы второй строки этой таблицы получаются по формулам .

Аналогично определяется условная вероятность случайной величине Y принять значение  при условии :

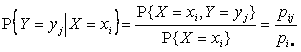
Пример 2.2.20. Закон распределения случайного вектора  задан таблицей:

Описать условные законы распределения: 1) случайной величины X при условии ; 2) случайной величины Y при условии .

Решение. Найдем безусловные законы распределения компонент X и Y:

1) Условные вероятности случайной величине X принять значения  () при условии  вычисляются по формулам:

,

,

.

Тогда условный закон распределения случайной величины X при условии  имеет вид:

2) Условные вероятности случайной величине Y принять значения  () при условии  вычисляются по формулам:

,

.

Тогда условный закон распределения случайной величины Y при условии  имеет вид:

 

В общем случае условную функцию распределения случайной величины X при условии  также естественно было бы определить формулой

.

Однако это не всегда возможно (например, для непрерывной случайной величины Y событие  имеет нулевую вероятность). Во избежание этих неприятностей, вместо события  рассматривается событие  и D устремляется к нулю. Тогда

.

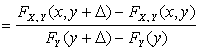Тогда условной функцией распределения  называется предел

.

Оказывается, такой предел всегда существует. Аналогично

Если случайная величина Y непрерывна, то условную функцию распределения можно определить следующим выражением:

.

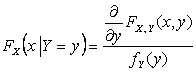Аналогично

.

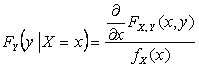В наиболее важных для приложений случаях вектор  представляет собой двумерную непрерывную случайную величину с совместной плотностью . Тогда

, .

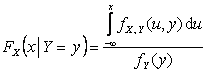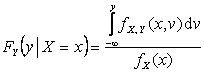Нетрудно видеть, что условная функция распределения  имеет производную по x, т.е. существует условная плотность распределения случайной величины X при условии :

.

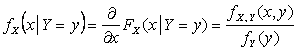Аналогично

.

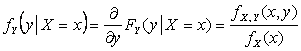Пример 2.2.21. В примере 2.2.10 была дана функция плотности :

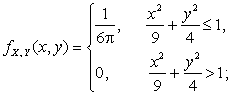
и найдены безусловные плотности распределения компонент X и Y:

  

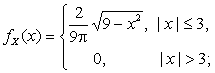
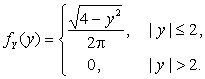
Найти условные плотности распределения компонент X и Y.

Решение. Условные плотности распределения компонент X и Y находятся по формулам , .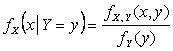

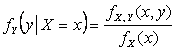Поэтому

 

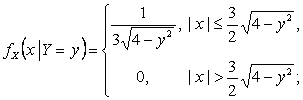
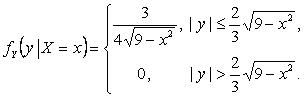
Таким образом, случайная величина X при условии  равномерно распределена на отрезке , а случайная величина Y при условии  равномерно распределена на отрезке . Условная плотность  не определена при , а условная плотность  не определена при .

Пример 2.2.22. Дан двумерный случайный вектор , где X – время появления в магазине первого покупателя в понедельник, а Y – время появления в магазине первого покупателя во вторник. Установлено, что , если . Найти: , , , . Установить, зависимы или нет случайные величины X и Y.

Решение. Найдем вначале функцию распределения случайного вектора :

, ;

 в остальных случаях.

Тогда по свойству 4 совместной функции распределения  получим:

 при ,  при .

Отсюда  при ,  при .

Найдем теперь условные функции распределения компонент:

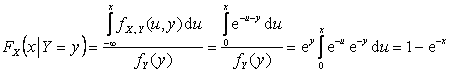 при ,

аналогично 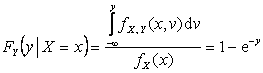 при .

Получим теперь условные плотности компонент:

 при ,

 при .

Поскольку , , то . Поэтому случайные величины X и Y независимы. Это означает, что появление в магазине первого покупателя во вторник не зависит от того, когда в магазин пришел первый покупатель в понедельник.

Ответ: при положительных x и y , , , ; случайные величины X и Y независимы.

Пример 2.2.23. Известна плотность совместного распределения непрерывной двумерной случайной величины :

.

Найти: 1) плотности распределения компонент X и Y; 2) условные плотности распределения компонент X и Y.

Решение. 1) Найдем вначале плотность распределения компоненты X:

.

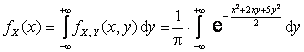Вынося за знак интеграла множитель , не зависящий от переменной интегрирования y, и дополнив оставшийся показатель степени до полного квадрата, получим:

.

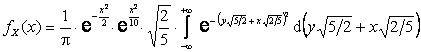Учитывая, что интеграл Пуассона , найдем плотность распределения компоненты X:

.

Аналогично найдем плотность распределения компоненты Y:

.

2) Найдем условные плотности распределения компонент X и Y. Выполнив элементарные выкладки, получим:

,.

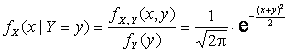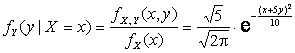Ответ: 1) , ;

2) , .

 

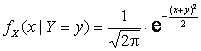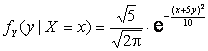2.2.7. Условные числовые характеристики случайных векторов. Регрессия

Определение. Условным математическим ожиданием одной из случайных величин, входящих в двумерный случайный вектор , называется ее математическое ожидание, вычисленное при условии, что другая случайная величина приняла определенное значение.

Если случайные величины X и Y дискретны, то условные математические ожидания вычисляются по формулам:

, .

Если случайные величины X и Y непрерывны, то условные математические ожидания вычисляются по формулам:

, .

Определение. Условное математическое ожидание случайной величины Y при заданном значении , т.е. , называется регрессией Y на x. Условное математическое ожидание случайной величины X при заданном значении , т.е. , называется регрессией X на y.

Графики этих зависимостей от x и y называются линиями регрессии Y на x (рис. 2.2.8 а) и X на y (рис. 2.2.8 б) соответственно.

                

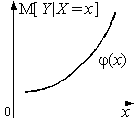
а                                              б

Рис. 2.2.8.

Пример 2.2.24. Закон распределения случайного вектора  задан таблицей:

Построить регрессии Y на x и X на y.

Решение. Найдем законы распределения компонент X и Y:

 

Построим вначале регрессию Y на x.

1) , , , отсюда .

2) , , , отсюда .

3) , , , отсюда .

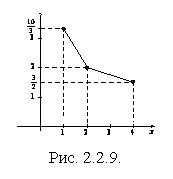
Графическое изображение регрессии Y на x показано на рис. 2.2.9.

Построим теперь регрессию X на y.

1) , , , отсюда .

2) , , , отсюда .

3) , , , отсюда .

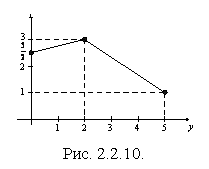
Графическое изображение регрессии X на y показано на рис. 2.2.10.

Для наглядности значения условного математического ожидания на рис. 2.2.9 и 2.2.10 соединены отрезками прямых.

Замечание 1. Для независимых случайных величин линии регрессии Y на x и X на y параллельны координатным осям, т.к. математическое ожидание каждой из них не зависит от того, какое значение приняла другая случайная величина. Линии регрессии могут быть параллельны координатным осям и для зависимых случайных величин, если только математическое ожидание каждой из них не зависит от того, какое значение приняла другая случайная величина.

Замечание 2. По аналогии с условными математическими ожиданиями можно рассматривать условные моменты. Например, условные дисперсии ,  и т.д.

Пример 2.2.25. В примере 2.2.10 была дана функция плотности :

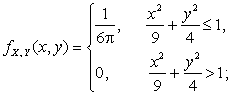
и найдены условные плотности распределения компонент X и Y (пример 2.2.21):

 

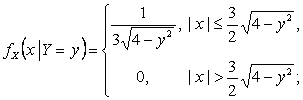
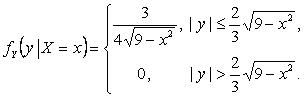
Найти регрессии Y на x и X на y, а также условные дисперсии компонент X и Y.

Решение. Условные математические ожидания вычисляются по формулам: , . Поэтому

,

.

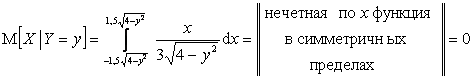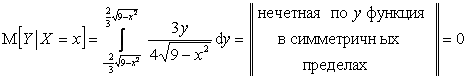Заметим, что при вычислении условных математических ожиданий можно было воспользоваться тем, что случайная величина X при условии  равномерно распределена на отрезке , а случайная величина Y при условии  равномерно распределена на отрезке .

Действительно, для равномерно распределенной на отрезке  случайной величины математическое ожидание равно , а дисперсия равна . Отсюда, очевидно,  при ,  при . Тогда условные дисперсии равны:

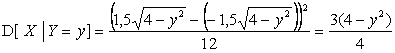 при ,

 при .

Ответ: ,  при ;

,  при .

 

2.2.8. Двумерное нормальное распределение

 

На практике часто встречаются двумерные случайные величины, распределение которых нормально.

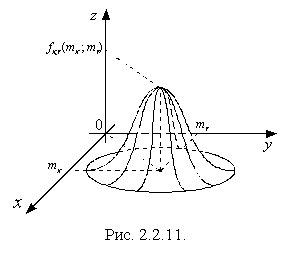
Определение. Нормальным законом распределения на плоскости называется распределение вероятностей двумерной случайной величины , функция плотности которой имеет вид

.

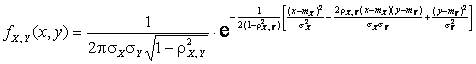Итак, нормальный закон на плоскости определяется пятью параметрами: . Смысл этих параметров: математические ожидания и средние квадратические отклонения компонент, а также коэффициент корреляции.

Пример 2.2.26. Доказать, что для нормально распределенных компонент двумерной случайной величины  понятия независимости и некоррелированности равносильны.

Решение. Действительно, пусть компоненты X и Y некоррелированны (), тогда плотность  принимает вид:

.

Отсюда очевидно, что

.

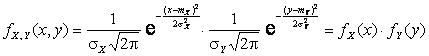Значит, компоненты X и Y независимы.

Обратное утверждение также выполняется (из независимости компонент X и Y всегда следует их некоррелированность).

Условные законы распределения случайных величин X и Y:

,

.

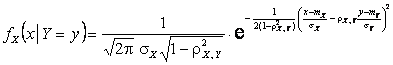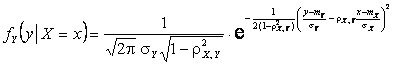Нетрудно видеть, что каждый из условных законов распределения также является нормальным с условным математическим ожиданием и условной дисперсией, вычисляемыми по формулам:

,     ;

,     .

Замечание. Из формул для условных математических ожиданий видно, что для системы нормально распределенных случайных величин X и Y линии регрессии Y на x и X на y представляют собой прямые линии, т.е. в данном случае регрессия всегда линейна.

В геометрической интерпретации график  двумерного нормального распределения представляет собой холмообразную поверхность, вершина которой находится в точке . Аппликата этой вершины равна 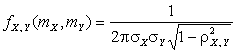 (рис. 2.2.11). Сечения поверхности  плоскостями, параллельными плоскости xOy, представляют собой эллипсы.

Определение. Нормальное распределение называется круговым с центром в точке , если случайные величины X и Y некоррелированны () и .

Пример 2.2.27. Случайная точка  на плоскости xOy распределена по двумерному нормальному закону с центром рассеивания , средними квадратическими отклонениями ,  и коэффициентом корреляции . Вычислить вероятность попадания случайной точки  в прямоугольник с вершинами , , , .

Решение. Поскольку коэффициент корреляции , то плотность  представляется в виде

.

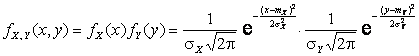С учетом того, что , , , , получим:

.

Поэтому , или

.

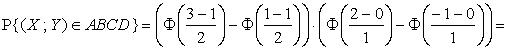
Ответ: .

Пример 2.2.28. Случайные величины X и Y независимы и распределены по нормальному закону. Известно, что , , . Найти радиус R круга с центром в точке , вероятность попадания в который случайной точки  равна 0,997.

Решение. Поскольку случайные величины X и Y независимы, то

.

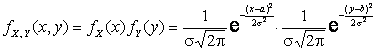Вероятность  попадания случайной точки  в круг D с центром в точке  и радиусом R вычисляется следующим образом:

.

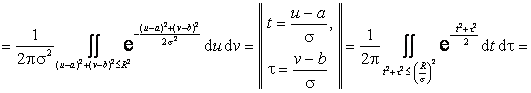
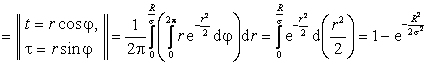Теперь, решая уравнение , получим . Отсюда .

Ответ: .

Пример 2.2.29. Заданы следующие характеристики двумерного нормального вектора : , , , , . 1) Записать выражения для плотности распределения вероятностей  и условных плотностей компонент , . 2) Составить уравнения регрессий Y на x и X на y. 3) Найти условные дисперсии компонент X и Y.

Решение. 1) По определению двумерного нормального вектора:

.

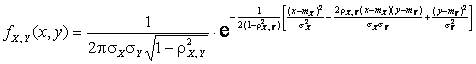С учетом того, что , , , , , выражение для  примет вид:

.

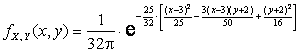Условные законы распределения случайных величин X и Y:

,

.

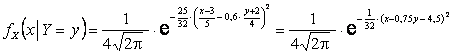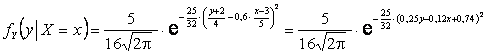2) Условные математические ожидания равны:

,

.

Таким образом, уравнение регрессии X на y имеет вид , а уравнение регрессии Y на x имеет вид .

3) Условные дисперсии равны:

,

.

Ответ: 1) ,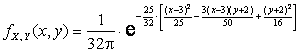

, .

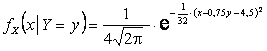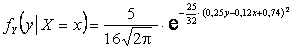2) Уравнение регрессии X на y: , уравнение регрессии Y на x: . 3) , .

 

Упражнения

2.2.23. Закон распределения случайного вектора  задан таблицей:

Описать условные законы распределения и найти условные математические ожидания: 1) случайной величины Y при условии : 2) случайной величины X при условии .

2.2.24. Известна плотность совместного распределения непрерывной двумерной случайной величины :

.

Найти: 1) константу C; 2) плотности распределения компонент X и Y; 3) условные плотности распределения компонент X и Y.

2.2.25. Известна плотность совместного распределения непрерывной двумерной случайной величины :

.

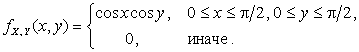Доказать независимость компонент X и Y, найдя плотности и условные плотности их распределения.

2.2.26. Двумерный случайный вектор  распределен равномерно внутри трапеции с вершинами , , , . Найти: 1) плотность распределения случайного вектора ; 2) плотности распределения компонент X и Y; 3) условные плотности распределения компонент X и Y.

2.2.27. Случайная точка  на плоскости xOy распределена по двумерному нормальному закону с центром рассеивания , средними квадратическими отклонениями ,  и коэффициентом корреляции . Вычислить вероятность попадания случайной точки  в прямоугольник с вершинами , , , .

2.2.28. На станке-автомате изготавливается деталь цилиндрической формы. Полученные в результате обработки длина L и радиус R детали являются независимыми случайными величинами, распределенными по нормальным законам с характеристиками:  мм,  мм,  мм,  мм. Установить процент бракованных деталей, если деталь считается годной, когда ее размеры определяются условиями:

 мм,  мм.

2.2.29. Производится стрельба по точечной (малоразмерной) цели, зона поражения которой представляет собой круг радиуса R с центром в начале координат. Рассеивание точки попадания снаряда – нормальное круговое с параметрами , . Сколько выстрелов надо произвести, чтобы поразить цель с вероятностью, не мéньшей 0,95?

 

 

Ответы к упражнениям

2.2.23. 1) Условный закон распределения Y при условии :

Условное математическое ожидание: .

2) Условный закон распределения X при условии :

Условное математическое ожидание: .

2.2.24. 1) ; 2) , ;

2) , .

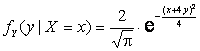2.2.26. 1) 

2) 

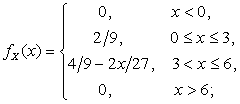
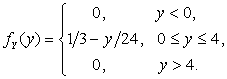
3) При :

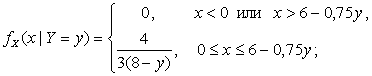
при ,  условная плотность  не определена.

При :

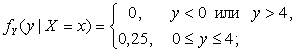
при :

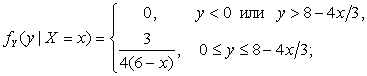
при ,  условная плотность  не определена.

2.2.27. .

2.2.28. %.

2.2.29. .