3. Законы больших
чисел и предельные теоремы теории вероятностей.
3.1. Законы больших чисел.
Ряд утверждений и теорем в теории
вероятностей объединены общим названием: законы
больших чисел.
Эти законы делятся на две группы. К первой
группе относятся утверждения, касающиеся оценок вероятностей больших отклонений
случайной величины Х от ее
математического ожидания, справедливые для любого распределения. Суть этой
группы законов можно выразить краткой формулой: большие отклонения от mX мало вероятны. Ко второй группе законов относятся утверждения о сходимости некоторых
последовательностей случайных величин (теорема Чебышева и ее обобщения).
Неравенства Чебышева.
Первое неравенство Чебышева.
Пусть Х – случайная величина с
конечным mX Þ
(3.1.1)
Пусть, для
определенности, Х-СВНТ. Запишем по определению математическое ожидание от модуля
случайной величины X :
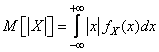
Выберем произвольное e>0, разобьем маршрут интегрирования на два непересекающиеся интервала и
воспользуемся свойством аддитивности интеграла по области.
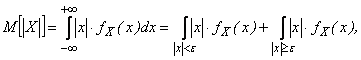
В силу неотрицательности
подинтегральной функции получаем
,
откуда следует (3.1.1). 
Следствие. Пусть Х 
0 Þ по одному из свойств математического ожидания Þ mX 0 Þ уравнение (3.1.1) перепишется в
виде:
(3.1.2)
Второе неравенство Чебышева (в
центрированной форме).
Пусть случайная величина Х имеет
конечные mX и 
Þ
Þ
(3.1.3)
Обозначим, как и ранее в главе 2, 
-центрированная случайная величина. Учитывая очевидное
равенство
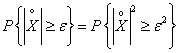
и применяя доказанное выше первое неравенство Чебышева (3.1.1), получим:
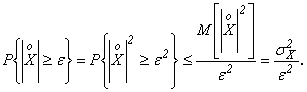
что и требовалось доказать.►
Пример 3.1.1. Пусть X-число бракованных
изделий из 100 наудачу отобранных из большой партии, поступившей в продажу. За
большой период посчитано, что в среднем для этого вида изделий брак составляет
1%. Оценить вероятность события {X 5 }.
Т.к. Х>0 и по условию mX=0,01×100=1,то по следствию из первого неравенства Чебышева Þ P{X 5}
Пример 3.1.2. Пусть в условиях примера (3.1.1) известно, что 
.Оценить P{X 5}.
Заметим, что в
силу условия X>0,
P{X 5} P{|X-1|4}
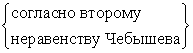
Заметим, что вероятность
существенно уменьшилась!
Пример 3.1.3 Предположим, X~PU(l=1), что
хорошо согласуется с данными задачи (одним из признаков этого является
равенство: mX=) и
соответствует закону редких явлений. Оценим снова вероятность события 
.
P{X 5}=
Это более, чем в 17 раз меньше предыдущей оценки!
Пример 3.1.4. В условиях примера 3.1.2. оценить вероятность события {X2}.
◄
Очевидно, что в силу условия 
имеем следующую
цепочку отношений между событиями
. (3.1.4)
Действительно,
откуда и следует (3.1.4).
Отсюда по
закону поглощения получаем
,
т.е.
получили тривиальный результат ►
Сделаем
некоторые выводы. Последние примеры показывают, что чебышевские оценки сверху вероятностей больших отклонений
случайной величины X
от ее математического ожидания являются довольно грубыми, что является
платой за незнание закона распределения сл.вел. X. На практике неравенства
Чебышева имеет смысл применять при условии 
. Однако теоретическое значение неравенств (3.1.1) – (3.1.3)
большое, что будет ясно из дальнейшего.
Еще раз
отметим, что рассмотренные выше примеры касались оценок сверху больших отклонений. Для получения оценок снизу следует перейти в неравенствах
(3.1.1) – (3.1.3) к противоположным событиям. Например из (3.1.3) получаем:
(3.1.5)
Пример 3.1.5 Средняя длина детали, производимой
на конвейерной линии, равна
◄
Пусть X –длина случайно взятой детали. Очевидно, что события 
и 
равносильны. Поэтому,
согласно неравенству (3.1.5) P1–
►
Пример 3.1.6. В условиях предыдущего примера
оценить снизу вероятность события {49<X<52}.
◄
Очевидно, что {49<X<52} 
{48<X<52}=
. Поэтому по свойству вероятности
. ►
Пример 3.1.7. Случайная величина X
дискретного типа задана законом распределения
|
|
0,3 |
0,6 |
|
|
0,2 |
0,8 |
а)
Используя неравенство Чебышева, оценить снизу вероятность события {
}.
б) Найти
точное значение вероятности указанного события.
◄ а)
Находим дисперсию: 
0,09*0,2+0,36*0,8-0,542=0,0144.
Далее,
согласно неравенству (3.1.5), получаем:
P{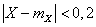}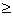1–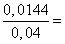
1–0,36=0,64.
б)
Используем закон распределения и цепочку очевидных равенств
P{}=P{0,34<X<0,74}=P{X=0,6}=0,8.
►
Пример 3.1.8. Устройство состоит из 10
независимо работающих элементов. Вероятность отказа каждого элемента за время t равна 0,03.
а) Оценить
вероятность события 
, используя неравенство Чебышева.
б) Найти
точное значение указанной вероятности.
◄ а)
Согласно постановке эксперимента 
, где n=10, p=0,03. Поэтому 
=0,5; 
=
=0,5*0,93. Далее используя (3.1.5), получаем
=0,88123.
б) Для точного ответа на вопрос используем биномиальный закон и формулу Бернулли:
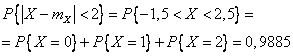
Пример 3.1.9. Игральная кость подбрасывается 6
раз. Пусть X – число выпадений четной цифры.
а) Оценить
по Чебышеву вероятность события 
.
б) Найти точное
значение указанной вероятности.
◄ а)
По условию эксперимента 
, где n=6, p=0.3. Отсюда следует: 
, 
=1,3. Далее согласно неравенству (3.1.3):
.
б)
Используем закон распределения:
=2
(1/2)6=1/32. ►
Анализируя
результаты последних трех примеров обнаруживаем следующую закономерность:
оценки по Чебышеву сверху всегда
завышены по сравнению с точными значениями вероятности, в то время как оценки снизу – занижены.
Упражнения.
3.1.7. Средний срок службы
автомобильной свечи зажигания 4 года. Оценить снизу вероятность того, что
данная свеча прослужит не более 8 лет.
3.1.8.
Среднее значение расхода воды в некотором малом населенном пункте составляет
3.1.9. В
сентябре в среднем наблюдается 7 дождливых дней. Оценить вероятность того, что
в сентябре 2007г. число дождливых дней будет больше 10.
3.1.10.
Пусть к данным задачи (3.1.7) добавлена информация, что 
=0,5 года. Оценить ту же вероятность.
3.1.11.*
Неотрицательные случайные величины X
и Y независимы, причем mX=6, mY=4, =1,5, 
=2. Оценить снизу вероятности событий: 
, 
.
Ответы к упражнениям
3.1.7. 0,3.
3.1.8.
0,583.
3.1.9.
0,727.
3.1.10.
0,984.
3.1.11. 
, 
. Указание. Использовать линейность оператора математического
ожидания. Для вычисления 
использовать свойство
оператора дисперсии (формула (), гл.2).
Задание для самостоятельной работы
[1] 18.542
– 18.548
Понятие сходимости по вероятности.
Определение. Последовательность случайных
величин 
сходится к случайной величине Х по вероятности при n®
, если 
(
) (3.1.6)
Достаточное условие сходимости по вероятности: 
Здесь {
} – зависящая от 
неотрицательная
неслучайная последовательность.
Замечание 1. В частных случаях в качестве
предельной величины может выступать и не случайная величина (например M[X]).
Замечание 2. Для сходимости по вероятности принято краткое
обозначение
.
Замечание 3. Сходимость по вероятности
принципиально отличается от обычного понятия сходимости неслучайных
последовательностей.
Пример 3.1.10. Рассмотрим
следующую последовательность случайных величин 
, где закон распределения Хn
описывается таблицей.
|
|
0 |
|
|
|
|
|
a) Показать, что 
б) Можно ли утверждать, что последовательность реализаций
данной случайной последовательности сходится к 0 в обычном смысле?
а) В силу неотрицательности 
имеем следующую
цепочку равенств:
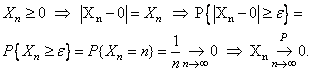
Таким образом, утверждение в пункте а) доказано.
б) Пусть эксперимент проведен и реализовалась последовательность x1, x2,…, xn,
где каждое xn Î {0,n} Þ на n-ом месте этой последовательности при 
может оказаться число n (поскольку вероятность этого события
ненулевая) Þ ни одна из сколь угодно малых окрестностей точки x=0 не может считаться "ловушкой" для последовательности
{xn}.Таким образом, нельзя считать, что последовательность
реализаций сходится к нулю в обычном смысле.
Пусть {Xn} –
последовательность случайных величин с конечными математическими ожиданиями и
дисперсиями. Для любого nÎN построим последовательность среднеарифметических 
, Þ получим последовательность Y1,Y2…Yn.,…
Определение. Говорят, что к последовательности {Xn} применим закон больших чисел, если 
Теорема 3.1.1 (закон больших чисел в формулировке Чебышева).
Пусть для
последовательности {Xn} выполняются следующие условия:
1)
Элементы последовательности попарно
независимы;
2)
=0.
Тогда для {Xn} выполняется закон больших чисел.
Согласно второму неравенству Чебышева в
центрированной форме:
Вычислим дисперсию среднего арифметического:
=
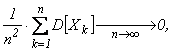
что следует из условия 2) теоремы.
Используем достаточное условие сходимости по вероятности:
Замечание 1. Теорема
Чебышева остается верной, если заменить попарную независимость на попарную
некоррелированность.
Замечание 2. Условие
некоррелированности так же можно снять, но тогда придется вводить более жесткие условия для дисперсии (см.
теорему Маркова в [3]).
Замечание 3. Имеют место следующие частные
случаи проявления закона больших чисел:
1) 
то есть дисперсии членов последовательности равномерно
ограничены Þ условие 2) выполняется;
2) все Xk
попарно независимы, одинаково распределены и имеют конечную дисперсию
В последнем случае закон больших чисел формулируется
следующим образом: “среднее
арифметическое первых n членов последовательности сходится по вероятности
к их общему мат.ожиданию”. В краткой записи:
Действительно,
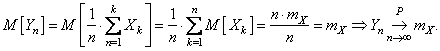
Теорема 3.1.2. (Закон больших чисел в формулировке
Бернулли.
Пусть Xn - число
успехов в n опытах по схеме Бернулли
с вероятностью успеха в одном опыте, равным p
(в краткой записи:Xn~B(n,p)). Обозначим
-относительная частота успехов. Тогда справедливо следующее
утверждение:
При увеличении числа опытов по схеме Бернулли относительная частота
успехов сходится по вероятности к
вероятности успеха в одном опыте.
Обозначим Ik
– индикатор успеха в k-ом опыте.
Очевидно, что Ik~B(1,P), kÎN. При любом n элементы последовательности
I1,I2…In – независимы в совокупности, а
потому и попарно независимы. Условие 1) теоремы Чебышева выполняется. Кроме
того: M[Ik]=p, D[Ik]=p×q, 
Þ выполняется частный случай 2) теоремы Чебышева Þ
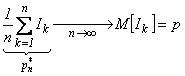
Теорема Бернулли играет большую роль в математической статистике,
составляя основу для оценивания неизвестной вероятности событий в реальных
экспериментах.
Пример 3.1.11. Случайная двоичная последовательность, вырабатываемая на ЭВМ, делится на
группы из одинаковых символов (нулей и единиц). Обозначим 
- число знаков в i-ой
группе; 
- среднее число знаков
в серии, вычисленное по n сериям.
Доказать, что последовательность 
сходится по вероятности
к 2.
◄ Из
условия следует, что последовательность 
- независимые случайные
величины одинаково распределенные по закону Гео(p=0,5). Как было показано в главе 2, для геометрического
распределения
=
=2; 
=
.
Таким
образом, удовлетворяются условия частной теоремы Чебышева (случай 2))
Отсюда следует, что
=2, что и требовалось
доказать ►
Пример 3.1.12. В последовательности 
случайные величины 
попарно независимы и
распределены по закону 
. Применим ли к этой
последовательности закон больших чисел?
◄
Используя известные характеристики равномерного распределения, получаем: 
=0, 
=
. Проверим второе
условие теоремы Чебышева:
.
Таким
образом, условие 2) не выполняется и данная последовательность не подчиняется
закону больших чисел.►
Пример 3.1.13. (сборка точных механизмов).
Пусть - случайная длина детали,
сходящей с конвейера. Известны ее основные характеристики:
=10 см, ==0,04 см2
Относительную
точность изготовления детали можно характеризовать отношением 
. Производится сборка
9 подобных деталей (т.е. их длины складываются). Обозначим 
. Вычислить относительную точность для Y, т.е.
отношение 
.
◄
Считая, что длина каждой изготовленной детали не зависит от остальных и
используя свойства операторов матожидания и дисперсии, получаем:
.
Отсюда
следует: =
. Таким образом,
относительная точность собранной детали повысилась в 3 раза. ►
Из
рассмотренных примеров можно сделать следующий вывод: проявление закона больших
чисел связано главным образом с тем, что сумма конечного числа независимых
случайных слагаемых имеет меньший относительный разброс, измеряемый отношением
С.К.О. к математическому ожиданию, чем у отдельно взятого слагаемого.
Задание для самостоятельной работы
Решить задачи 18.550 – 18.555 из задачника [1], предварительно прочитав теоретическую преамбулу параграфа 5 и разобрав решение примера 1.
