3.2 Центральная предельная теорема и ее применения.
Теорема 3.2.1 (Центральная предельная теорема в
формулировке. Ляпунова) Пусть для
последовательности случайных величин ![]() выполняются условия:
выполняются условия:
1)при любых n случайные величины ![]() - независимы в
совокупности;
- независимы в
совокупности;
2)одинаково распределены;
3)существует ![]() ,
, ![]() .
.
Обозначим: 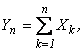
![]() ,
,![]()
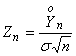 , где
, где ![]() .
.
Тогда ![]()
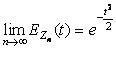
Замечание 1. Мы дали одну из простейших
формулировок центральной предельной теоремы. Все более поздние формулировки
связаны с устранением пункта 2), но тогда усложняется условие 3). Чаще всего
оно формулируется в виде условия Линдеберга (гарантирует, что все слагаемые ![]() вносят равномерно
малый вклад в общую дисперсию).[3]
вносят равномерно
малый вклад в общую дисперсию).[3]
Замечание
2. Из утверждения теоремы согласно
свойству 7 характеристической функции следует, что предельным законом для ![]() при
при ![]() будет нормальный
будет нормальный ![]() .
.
Центральная предельная теорема играет
большую роль в приложениях теории вероятностей. Одним из ярких примеров
применения этой теоремы на практике является баллистика, изучающая явления
рассеивания снарядов при стрельбе по цели.
На траекторию полета снаряда
действует множество независимых факторов: колебания атмосферного давления,
влажности, температуры, отклонения величины заряда и веса снаряда от номинала,
ошибка прицеливания, сила ветра на различных высотах и т.д. Результатом этих
многочисленных воздействий, каждое из которых вносит свой равномерно малый
вклад в общую сумму (ограниченность дисперсий!)
является то, что отклонение точки попадания от цели удивительно точно
описывается двумерным нормальным законом распределения.
Другим примером применения центральной предельной теоремы является теория
и практика измерений. Всякое измерение неизбежно сопряжено с погрешностями.
Реально наблюдаемая погрешность измерения является суммой элементарных
погрешностей, вызванных многочисленными факторами, каждый из которых лишь
незначительно влияет на результат. В силу центральной предельной теоремы
результирующая погрешность должна быть приближенно нормальной. Это
обстоятельство играет решающую роль в разработке эффективных методов обработки
опытных данных в математической статистике.
Пример 3.2.1. Пусть ![]() - последовательность
независимых одинаково распределенных случайных величин с конечными дисперсиями,
- последовательность
независимых одинаково распределенных случайных величин с конечными дисперсиями,
![]() ,
, ![]() . Вычислить
. Вычислить ![]() , если
, если
а) ![]() .
.
б) ![]() .
.
в) ![]() .
.
◄ а) Пусть ![]() >0,
>0, ![]() ,
, ![]() 1,2,…Преобразуем неравенство под знаком
1,2,…Преобразуем неравенство под знаком ![]() :
:
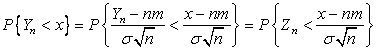 .
.
Поскольку 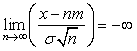 при
при ![]() , а предельным законом для
, а предельным законом для ![]() при
при ![]() является нормальный,
то получаем:
является нормальный,
то получаем: ![]() =0.►
=0.►
б) Ответ: ![]() =1.
=1.
в) Ответ: ![]() =0,3.
=0,3.
Пример 3.2.2. Пусть ![]() - последовательность
независимых одинаково распределенных случайных величин с конечными дисперсиями,
- последовательность
независимых одинаково распределенных случайных величин с конечными дисперсиями,
![]() . Доказать, что
. Доказать, что ![]()
![]() .
.
Указание:
преобразовать неравенство под знаком ![]() к неравенству со случайной
величиной
к неравенству со случайной
величиной ![]() и воспользоваться
результатом ЦПТ.
и воспользоваться
результатом ЦПТ.
Пример 3.2.3. Пусть ![]() - последовательность
независимых одинаково распределенных случайных величин с нулевыми
математическими ожиданиями и конечными дисперсиями,
- последовательность
независимых одинаково распределенных случайных величин с нулевыми
математическими ожиданиями и конечными дисперсиями, ![]() . Найти
. Найти ![]() , если известно, что
, если известно, что
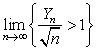 =1/3.
=1/3.
Ответ: ![]() 2,23.
2,23.
3.3. Предельные теоремы в схеме Бернулли.
Одним из важных для практики следствий центральной предельной теоремы
является так называемая асимптотическая нормальность некоторых известных
распределений. В частности, для биномиального распределения указанное свойство
было доказано независимо А.Муавром (1730г.) и П.Лапласом (1812) задолго до
появления ЦПТ и составило содержание двух теорем: так называемой локальной и
интегральной теорем Муавра-Лапласа.
Сформулируем их.
Теорема 3.3.1.( локальная теорема). Пусть ![]() - число успехов в n опытах по схеме Бернулли, p - вероятность
успеха в одном опыте,
- число успехов в n опытах по схеме Бернулли, p - вероятность
успеха в одном опыте, ![]() - фиксированная величина.
Тогда для достаточно больших n
справедлива приближенная формула:
- фиксированная величина.
Тогда для достаточно больших n
справедлива приближенная формула:
![]() /
/![]() , (3.3.1)
, (3.3.1)
где 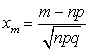 , а
, а ![]()
![]() - плотность
нормального стандартизованного распределения.
- плотность
нормального стандартизованного распределения.
◄
Доказательство основано на применении формулы Стирлинга для факториалов в
формуле Бернулли и вычислении предела при ![]() . Ввиду громоздкости вычислений мы этого доказательства не
приводим (см., например, [3]).►
. Ввиду громоздкости вычислений мы этого доказательства не
приводим (см., например, [3]).►
Теорема 3.3.2 (интегральная теорема
Муавра-Лапласа). Пусть снова ![]() - число успехов в n опытах по схеме Бернулли, p - вероятность успеха в одном опыте. Тогда при
условии
- число успехов в n опытах по схеме Бернулли, p - вероятность успеха в одном опыте. Тогда при
условии ![]() для вероятности
попадания случайной величины
для вероятности
попадания случайной величины ![]() на промежуток
на промежуток ![]() справедлива
приближенная формула:
справедлива
приближенная формула:
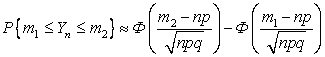 , (3.3.2)
, (3.3.2)
где ![]() - интеграл вероятности (функция нормального
стандартизованного распределения).
- интеграл вероятности (функция нормального
стандартизованного распределения).
◄ Доказательство, данное Муавром и Лапласом опирается на локальную
теорему и здесь не приводится (см.например, [3] ).►
Покажем, что интегральная теорема является простым следствием центральной
предельной теоремы. Действительно, поскольку по условию ![]() ~B(n, p),
то можно использовать представление
~B(n, p),
то можно использовать представление 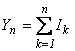 , где Ik
~B(1, p) – индикатор успеха в k-м
опыте по схеме Бернулли.Не трудно убедиться, что последовательность I1 ,I2
,…,
, где Ik
~B(1, p) – индикатор успеха в k-м
опыте по схеме Бернулли.Не трудно убедиться, что последовательность I1 ,I2
,…,![]() удовлетворяет всем условиям ЦПТ (см. ход доказательства теоремы 3.1.2.). Поэтому для стандартизованной
случайной величины
удовлетворяет всем условиям ЦПТ (см. ход доказательства теоремы 3.1.2.). Поэтому для стандартизованной
случайной величины 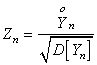
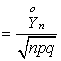 справедливо
утверждение теоремы о предельном нормальном законе распределения. Отсюда,
учитывая очевидное равенство
справедливо
утверждение теоремы о предельном нормальном законе распределения. Отсюда,
учитывая очевидное равенство
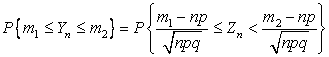 , получаем формулу (3.3.2).
, получаем формулу (3.3.2).
Пример 3.3.1. 100 раз подброшена правильная монета. Применяя локальную или интегральную
теоремы Муавра-Лапласа, вычислить приближенно вероятность того, что герб
выпадет а) ровно 50 раз; б) ровно 35 раз; в) от 45 до 65 раз.
◄ Пусть ![]() -число выпадений герба при 100 подбрасываниях монеты.
Очевидно, что
-число выпадений герба при 100 подбрасываниях монеты.
Очевидно, что ![]() . Далее находим:
. Далее находим: ![]() 50,
50, ![]() 3.
3.
а) 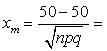 0. По формуле (3.3.1), используя таблицу значений функции
0. По формуле (3.3.1), используя таблицу значений функции ![]() (плотности нормального стандартизованного распределения),
находим:
(плотности нормального стандартизованного распределения),
находим:
![]() =0,39894
=0,39894![]() 5=0,0798.
5=0,0798.
б) 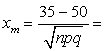 -3. Аналогично предыдущему, находим:
-3. Аналогично предыдущему, находим: ![]() 0,00089.
0,00089.
в) По формуле (3.3.2), используя таблицу интеграла вероятности и свойства
функции ![]() , находим:
, находим:
![]() 0,9763.►
0,9763.►
Пример 3.3.2 Компьютерная программа выдала 10000 случайных чисел из множества ![]() . Найти приближенное значение того, что число “нулей” будет
заключено между 940 и 1060.
. Найти приближенное значение того, что число “нулей” будет
заключено между 940 и 1060.
◄ По условию, числа 0,1,…,9, вырабатываемые генератором, имеют
дискретное равномерное распределение с вероятностью реализации каждого числа ![]() 0,1. Обозначим
0,1. Обозначим ![]() число нулей, появившихся в 10000 испытаниях по схеме
Бернулли. Очевидно, что
число нулей, появившихся в 10000 испытаниях по схеме
Бернулли. Очевидно, что ![]() . При этом
. При этом ![]() 10000;
10000; ![]() 30. Используем интегральную теорему Муавра-Лапласа. По
формуле (3.3.2) получаем:
30. Используем интегральную теорему Муавра-Лапласа. По
формуле (3.3.2) получаем:
![]() 0,93.►
0,93.►
Пример 3.3.3. Найти такое натуральное число ![]() , чтобы с вероятностью, не меньшей 0,9, можно было
утверждать, что число мальчиков среди 900 новорожденных будет больше
, чтобы с вероятностью, не меньшей 0,9, можно было
утверждать, что число мальчиков среди 900 новорожденных будет больше ![]() (считать рождение
мальчика и девочки равновероятными и независимыми событиями).
(считать рождение
мальчика и девочки равновероятными и независимыми событиями).
◄ Обозначим ![]() - число мальчиков из
900 новорожденных. По условию можно считать, что
- число мальчиков из
900 новорожденных. По условию можно считать, что ![]() . Искомое число
. Искомое число ![]() должно удовлетворять
неравенству
должно удовлетворять
неравенству
![]() . Считая возможным нормальное приближение согласно
интегральной теореме Муавра-Лапласа, по формуле (3.3.2) получаем:
. Считая возможным нормальное приближение согласно
интегральной теореме Муавра-Лапласа, по формуле (3.3.2) получаем:
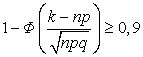 , что равносильно неравенству
, что равносильно неравенству
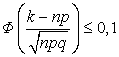 .
.
Так как значение вероятности в правой части меньше 0,5, то аргумент
функции ![]() отрицателен. Используя
свойство интеграла вероятности, из последнего неравенства находим:
отрицателен. Используя
свойство интеграла вероятности, из последнего неравенства находим: ![]() , откуда окончательно следует:
, откуда окончательно следует: ![]() .►
.►
Пример 3.3.4. После открытия Менделем законов наследственности многие ботаники
проводили опыты по скрещиванию желтого (гибридного) гороха с зеленым. По
известной гипотезе Менделя вероятность появления зеленого гороха в таких опытах
должна быть равна ![]() . Проведя 34153 опыта, в 8436 случаях получили зеленый горох.
Обозначим
. Проведя 34153 опыта, в 8436 случаях получили зеленый горох.
Обозначим ![]() - относительная
частота появления зеленого гороха. Ответить на следующие вопросы:
- относительная
частота появления зеленого гороха. Ответить на следующие вопросы:
1) Вычислить вероятность события ![]() .
.
2) Вычислить вероятность того, что при повторении такого же числа 34153
опытов отклонение относительной частоты от 0,25 не превзойдет величины,
полученной ботаниками.
◄ 1) По определению относительной частоты ![]() =
=![]() , где
, где ![]() - число успехов (число
появлений зеленого гороха) в
- число успехов (число
появлений зеленого гороха) в ![]() 34153 опытах по схеме Бернулли с вероятностью успеха в одном
опыте 0,23. Отсюда получаем:
34153 опытах по схеме Бернулли с вероятностью успеха в одном
опыте 0,23. Отсюда получаем: ![]() =34153
=34153![]() 0,25=8538,25;
0,25=8538,25; ![]() ;
; ![]() .
.
Далее используем формулу (3.3.2):
![]()
![]()
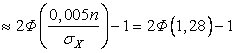 =0,7993.
=0,7993.
2) В опытах получено значение относительной частоты 8436/34153=0,247, что
соответствует величине отклонения от вероятности, равной 0,003,![]()
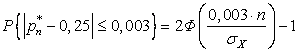 =0,7995►
=0,7995►
Пример 3.3.5. (продолжение). Сколько надо произвести опытов, чтобы с вероятностью не
меньшей 0,99 можно было утверждать, что отклонение относительной частоты от
0,25 не превзойдет 0,01?
◄ Вопрос сводится к решению неравенства
![]() относительно n. Используя
характеристики
относительно n. Используя
характеристики ![]() и
и ![]() из предыдущего
примера, преобразуем неравенство под знаком
из предыдущего
примера, преобразуем неравенство под знаком ![]() :
:
![]() .
.
Применяя к последнему неравенству интегральную теорему Муавра-Лапласа,
получаем: 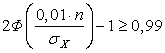 , откуда следует
, откуда следует 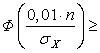 0,993.
0,993.
Далее с помощью таблицы квантилей нормального распределения находим: ![]() 80
80![]() 2,576, откуда следует:
2,576, откуда следует: ![]() ►
►
При качественной оценке условий применимости приближенных формул (3.3.1) и
(3.3.2) необходимо оценить величину остаточных членов при замене биномиальных
вероятностей на значения, получаемые с помощью формулы Стирлинга при конечном
значении ![]() . Точную величину абсолютной погрешности получить в этом
случае довольно сложно, но основной вывод заключается в том, что погрешность
составляет величину порядка
. Точную величину абсолютной погрешности получить в этом
случае довольно сложно, но основной вывод заключается в том, что погрешность
составляет величину порядка 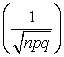 . Таким образом, для хорошего приближения нормальным законом
условия
. Таким образом, для хорошего приближения нормальным законом
условия ![]() недостаточно. Нужно,
чтобы
недостаточно. Нужно,
чтобы ![]()
![]() 1, что при больших
1, что при больших ![]() и значениях
и значениях ![]() или
или ![]() близких к 0 или 1,
может не выполняться.
близких к 0 или 1,
может не выполняться.
Основные рекомендации по практическому использованию формул (3.3.1) и
(3.3.2) для инженерных расчетов вкратце сводятся к следующему. При значениях ![]() 0,5 хорошие приближения, дающие относительную погрешность в
пределах 5% – 7%, получаются уже при
0,5 хорошие приближения, дающие относительную погрешность в
пределах 5% – 7%, получаются уже при ![]() 10. При этом, чем ближе значения
10. При этом, чем ближе значения ![]() (в формуле (3.3.1)) и
(в формуле (3.3.1)) и ![]() (в формуле (3.3.2)) к
значению
(в формуле (3.3.2)) к
значению ![]() , тем точнее получается результат.
, тем точнее получается результат.
Пример 3.3.6. 10 раз подброшена правильная монета. Вычислить вероятность того, что
выпадет ровно ![]() гербов (
гербов (![]() =0,1,…,10).
=0,1,…,10).
◄ Обозначим 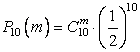 - точные значения
биномиальных вероятностей;
- точные значения
биномиальных вероятностей; ![]() - приближенные
значения, определяемые по формуле (3.3.1).
- приближенные
значения, определяемые по формуле (3.3.1).
В данном случае имеем: ![]() =5;
=5; ![]() =
=![]() =1,5811;
=1,5811; ![]() ;
;
![]() =
=![]() . Значения функции
. Значения функции ![]() находим из таблицы П2
задачника [1]. Результаты вычислений приведены в таблице 3.3.1.
находим из таблицы П2
задачника [1]. Результаты вычислений приведены в таблице 3.3.1.
Отсутствующие
в таблице значения вероятностей для ![]() восстанавливаются по
уже найденным благодаря свойству симметрии биномиального распределения
восстанавливаются по
уже найденным благодаря свойству симметрии биномиального распределения ![]() и четности функции
и четности функции ![]() :
: ![]() .
.
Таким
образом, мы видим, что наихудший по точности результат получается при ![]() =0 и
=0 и ![]() =10. При остальных значениях
=10. При остальных значениях ![]() относительная
погрешность приближения по локальной теореме Муавра-Лапласа не превышает 6% и
дает наилучший результат при
относительная
погрешность приближения по локальной теореме Муавра-Лапласа не превышает 6% и
дает наилучший результат при ![]() =4. ►
=4. ►
Таблица 3.3.1. (∆ - абсолютная
погрешность, δ – относительная погрешность в %)
|
|
|
|
∆ |
δ
|
|
0 |
0,00098 |
0,00171 |
0,00073 |
74,5% |
|
1 |
0,00977 |
0,01028 |
0,00051 |
5,22% |
|
2 |
0,04395 |
0,04150 |
0,00245 |
5,57% |
|
3 |
0,11719 |
0,11408 |
0,00311 |
2,65% |
|
4 |
0,20508 |
0,20690 |
0,00182 |
0,89% |
|
5 |
0,24609 |
0,25231 |
0,00622 |
2,53% |
При небольших значениях ![]() точность приближения
по интегральной теореме Муавра-Лапласа можно значительно повысить,
воспользовавшись так называемой поправкой Феллера в формуле (3.3.2) [] :
точность приближения
по интегральной теореме Муавра-Лапласа можно значительно повысить,
воспользовавшись так называемой поправкой Феллера в формуле (3.3.2) [] :
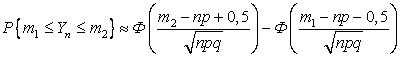 (3.3.3)
(3.3.3)
При этом следует иметь в виду, что точность приближений (3.3.2) и (3.3.3)
зависит не только от величины ![]() , но и от промежутка
, но и от промежутка ![]() .
.
Пример 3.3.7. Сделано 100 независимых выстрелов по цели с вероятностью попадания ![]() =0,23. Пусть
=0,23. Пусть ![]() - число попаданий при
100 выстрелах. Вычислить вероятности
- число попаданий при
100 выстрелах. Вычислить вероятности ![]() для трех промежутков: [15,35],
[20,30] и [30,40].
для трех промежутков: [15,35],
[20,30] и [30,40].
◄
Обозначим ![]() =
= - точное значение искомой вероятности по формуле
Бернулли;
- точное значение искомой вероятности по формуле
Бернулли; ![]() - нормальное
приближение, вычисленное по формуле (3.3.2);
- нормальное
приближение, вычисленное по формуле (3.3.2); ![]() - уточненное по
Феллеру приближение по формуле (3.3.3). Результаты вычислений с точностью до
4-х знаков после запятой приведены в таблице 3.3.2
- уточненное по
Феллеру приближение по формуле (3.3.3). Результаты вычислений с точностью до
4-х знаков после запятой приведены в таблице 3.3.2
Таблица 3.3.2 (![]() - относ.погрешность приближения
- относ.погрешность приближения ![]() ,
, ![]() - то же для
- то же для ![]() )
)
|
|
|
|
|
|
|
|
|
15 |
35 |
0,9852 |
0,9791 |
0,9845 |
0,62 |
0,07 |
|
20 |
30 |
0,7967 |
0,7519 |
0,7959 |
5,62 |
0,10 |
|
30 |
40 |
0,1492 |
0,1238 |
0,1492 |
17,02 |
0,0 |
Из таблицы
видно, что приближение с поправкой Феллера существенно улучшает точность,
особенно в ситуации, когда обычное приближение Муавра-Лапласа дает наихудший
результат. Последнее наблюдается, когда промежуток выбирается правее среднего
значения (на правом хвосте распределения).►
Упражнения
3.3.8.
Дисперсия каждой из 4500 независимых, одинаково распределенных случайных
величин равна 3. Вычислить приближенно вероятность ![]() того, что среднее
арифметическое этих величин отклонится от своего математического ожидания не
более, чем на 0,04,
того, что среднее
арифметическое этих величин отклонится от своего математического ожидания не
более, чем на 0,04,
а)
используя второе неравенство Чебышева;
б)
используя нормальное приближение как следствие из ЦПТ.
3.3.9.
Партия куриных яиц принимается, если 96% всех яиц удовлетворяет нормам приемки
(удовлетворяет стандарту). Считая, что число стандартных яиц в партии
подчиняется биномиальному закону, найти приближенно вероятность того, что при
контроле 200 яиц обнаружится не менее 190 стандартных.
3.3.10.
Сделано 100 независимых выстрелов по цели с вероятностью попадания ![]() =0,3. Обозначим
=0,3. Обозначим ![]() - число попаданий.
Вычислить вероятность события
- число попаданий.
Вычислить вероятность события ![]() , используя интегральную теорему Муавра-Лапласа и уточненную
формулу (3.3.3). Известно точное значение биномиальной вероятности указанного
события (
, используя интегральную теорему Муавра-Лапласа и уточненную
формулу (3.3.3). Известно точное значение биномиальной вероятности указанного
события (![]() =0,4469). Для каждого приближения вычислить относительную ошибку.
=0,4469). Для каждого приближения вычислить относительную ошибку.
3.3.11.
Пусть ![]() - сумма очков при
- сумма очков при ![]() подбрасываниях
игральной кости. Оценить вероятность события
подбрасываниях
игральной кости. Оценить вероятность события 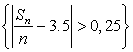 для двух значений
для двух значений ![]() :
: ![]() =35;
=35; ![]() =70 двумя способами: а) используя второе неравенство
Чебышева; б) считая возможным использовать нормальное приближение согласно ЦПТ.
=70 двумя способами: а) используя второе неравенство
Чебышева; б) считая возможным использовать нормальное приближение согласно ЦПТ.
3.3.12. С
конвейера сходит в среднем 85% изделий первого сорта. Сколько изделий
необходимо взять, чтобы с вероятностью, не меньшей 0,997, отклонение относительной
частоты появления изделия первого сорта в выбранной партии от вероятности
появления по абсолютной величине не превосходило 0,01? (Предполагаем, что
искомое значение ![]() достаточно велико,
чтобы можно было применить интегральную теорему Муавра-Лапласа).
достаточно велико,
чтобы можно было применить интегральную теорему Муавра-Лапласа).
3.3.13.
Вероятность, что посетителю понадобится обувь 44 размера равна 0,1. Магазин
ежедневно посещает 500 мужчин. Пусть ![]() - число посетителей из
500, затребовавших обувь 44 размера. Ответить на следующие вопросы.
- число посетителей из
500, затребовавших обувь 44 размера. Ответить на следующие вопросы.
1) Каково
среднее число затребованных пар обуви 44 размера?
2) Каково
среднеквадратическое отклонение этого числа?
3) Какова
вероятность, что в понедельник будет затребовано число пар, не превышающее
среднего значения?
4)
Учитывая, что среднего числа в какой-то день может не хватить в магазине, найти
такой гарантированный запас ![]() , который с вероятностью, не меньшей 0,95, окажется
достаточным, чтобы удовлетворить спрос покупателей.
, который с вероятностью, не меньшей 0,95, окажется
достаточным, чтобы удовлетворить спрос покупателей.
3.3.14.
(продолжение). Пусть запас в магазине обуви 44 размера составляет ![]() . Предположим, что 31 декабря образовался покупательский бум,
и в магазин пришло 625 покупателей. Какова вероятность, что запаса не хватит?
. Предположим, что 31 декабря образовался покупательский бум,
и в магазин пришло 625 покупателей. Какова вероятность, что запаса не хватит?
3.3.15. (продолжение). В каких границах (симметричных
относительно среднего значения) должно находиться число пар обуви 44 размера,
чтобы удовлетворить спрос покупателей с вероятностью 0,95?
3.3.16.
Обозначим ![]() , где
, где ![]()
Вычислить ![]() .
.
Ответы
к упражнениям
3.3.8. а) ![]() 0,30556; б)
0,30556; б) ![]() 0,76986.
0,76986.
3.3.9.
99984
3.3.10. 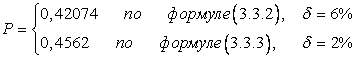
3.3.11. ![]() =33. а)
=33. а) ![]() 4/3 (не дает эффекта); б)
4/3 (не дает эффекта); б) ![]() 0,3869.
0,3869.
![]() =70. а)
=70. а) ![]() 0,667; б)
0,667; б) ![]() 0,2193.
0,2193.
3.3.12. ![]() 11247.
11247.
3.3.13. 1) ![]() =50; 2)
=50; 2) ![]() =6,708; 3) 0,5; 4)
=6,708; 3) 0,5; 4)![]() =62.
=62.
3.3.14.
0,5267.
3.3.13. [37,64].
3.3.16. 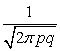
Задание
для самостоятельной работы
Решить
задачи: [1], гл.18, №№ 556, 557, 559, 561, 562, 563, 565, 566, 567, 569, 570.
Нормальная асимптотика закона
Пуассона.
Теорема 3.3.3. Пусть ![]() ,
, ![]() - стандартизованная
пуассоновская случайная величина. Тогда для характеристической функции
- стандартизованная
пуассоновская случайная величина. Тогда для характеристической функции ![]() справедливо
утверждение:
справедливо
утверждение: ![]() . На основании свойства 6) характеристической функции это
означает, что предельным законом для
. На основании свойства 6) характеристической функции это
означает, что предельным законом для ![]() при
при ![]() является нормальный
является нормальный ![]() .
.
◄
Доказательство см. [1], задача 18.572►
Из
утверждения теоремы следует, что при достаточно больших значениях параметра ![]() можно приближенно
аппроксимировать пуассоновское распределение нормальным.
можно приближенно
аппроксимировать пуассоновское распределение нормальным.
Пример 3.3.17. Для некоторого автопарка среднее
число автобусов ![]() , отправляемых в ремонт после месяца эксплуатации на
городских линиях, равно 4. Считая, что
, отправляемых в ремонт после месяца эксплуатации на
городских линиях, равно 4. Считая, что ![]() подчиняется закону
Пуассона с параметром
подчиняется закону
Пуассона с параметром ![]() =4, вычислить вероятности событий
=4, вычислить вероятности событий ![]() для
для ![]() двумя способами: по
точной формуле для пуассоновского распределения и в приближении нормальности.
двумя способами: по
точной формуле для пуассоновского распределения и в приближении нормальности.
◄
Обозначим ![]() - точное значение
искомой вероятности (находим по таблице П4 задачника []);
- точное значение
искомой вероятности (находим по таблице П4 задачника []);
![]() - в приближении нормальности.
Результаты вычислений представлены в таблице 3.3.3, где указаны относительные
погрешности вычислений по приближенной формуле.
- в приближении нормальности.
Результаты вычислений представлены в таблице 3.3.3, где указаны относительные
погрешности вычислений по приближенной формуле.
Таблица
3.3.3.
m
|
|
|
|
|
1 |
0,98168 |
0,9332 |
4,94 |
|
2 |
0,7619 |
0,8413 |
10,42 |
|
4 |
0,56653 |
0,5 |
11,7 |
|
6 |
0,21487 |
0,1587 |
26 |
Снова
наблюдается картина, аналогичная той, которая получается при аппроксимации
биномиального распределения нормальным (см.табл.3.3.2): точность приближения
резко падает при удалении левой границы промежутка ![]() от среднего значения
от среднего значения ![]() . Заметим однако, что значение
. Заметим однако, что значение ![]() =4 не является достаточно большим, чтобы гарантировать
хорошую точность нормального приближения ►
=4 не является достаточно большим, чтобы гарантировать
хорошую точность нормального приближения ►
Пример 3.3.18. Обследуются две группы деловых
людей. В первой группе (экологи) имеется в среднем 1% курящих. Во второй
(политики) – число курящих составляет в среднем 10%. Обозначим ![]() - число курящих для
каждой группы. Вычислить
- число курящих для
каждой группы. Вычислить ![]() .
.
◄
Очевидно можно считать, что ![]() , где
, где ![]() =0,01;
=0,01; ![]() =0,1. Таким образом, для первой группы выполняются условия:
=0,1. Таким образом, для первой группы выполняются условия: ![]() ,
, ![]() 1 и
1 и ![]() =2=
=2=![]() , то есть выполнены условия применимости теоремы Пуассона (закон
редких явлений). Используя пуассоновскую аппроксимацию биномиального распределения,
получаем:
, то есть выполнены условия применимости теоремы Пуассона (закон
редких явлений). Используя пуассоновскую аппроксимацию биномиального распределения,
получаем:
![]() =0,00003.
=0,00003.
Для второй
группы выполняются условия: ![]() =20,
=20, ![]() =
=![]() =4,24>1 и промежуток
=4,24>1 и промежуток ![]() содержит среднее
значение. Следовательно можно ожидать, что применение интегральной теоремы
Муавра-Лапласа даст приемлемую точность. Имеем:
содержит среднее
значение. Следовательно можно ожидать, что применение интегральной теоремы
Муавра-Лапласа даст приемлемую точность. Имеем: 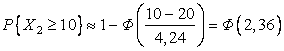 =0,9909.
=0,9909.
Заметим,
что если для второй группы принять за основу не биномиальное, а пуассоновское
распределение с ![]() =20
=20![]() 1, то применяя нормальную аппроксимацию непосредственно к
пуассоновскому распределению (теорема 3.3.3), получим:
1, то применяя нормальную аппроксимацию непосредственно к
пуассоновскому распределению (теорема 3.3.3), получим: 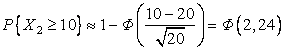 =0,9873. Заметим, что относительная погрешность данного
результата по сравнению с предыдущим составляет 0,34%.►
=0,9873. Заметим, что относительная погрешность данного
результата по сравнению с предыдущим составляет 0,34%.►
Задание
для самостоятельной работы
Для более
глубокого усвоения вопросов, связанных с понятием нормальной асимптотики
пуассоновского распределения, рекомендуется решить задачи 18.573 – 18.576 из
задачника [1]. Нормальная асимптотика закона хи-квадрат подробно рассмотрена в
задаче 18.577. Рекомендуется также решить задачу 18.578.
3.4. Дополнительные задачи, связанные с центральной предельной теоремой
В начале
приведем доказательство теоремы 3.2.1, важное в методическом отношении. Доказательство
основано на применении аппарата характеристической функции, свойства которой
подробно рассматривались в главе 2.
![]() Из условия 3) следует, что существуют
Из условия 3) следует, что существуют ![]() ,
,![]() .Проверим, что
.Проверим, что ![]() - стандартизованная
случайная величина.
- стандартизованная
случайная величина.
Действительно, 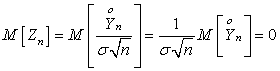 ,
,
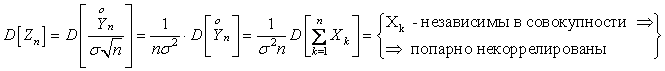 =
=![]()
![]()
Строим характеристическую функцию ![]() по этапам,
обозначенным стрелками:
по этапам,
обозначенным стрелками:
![]() Заметим, что по определению
Заметим, что по определению 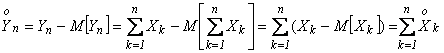 .
.
I этап. Ищем ![]() . Т.к. по условию 3) существует
. Т.к. по условию 3) существует ![]() Þ по свойству 4) характеристической
функции существует
Þ по свойству 4) характеристической
функции существует ![]() и
и ![]() . Разложим функцию
. Разложим функцию ![]() в ряд Тейлора до
членов второго порядка включительно с остаточным членом в форме Пеано Þ
в ряд Тейлора до
членов второго порядка включительно с остаточным членом в форме Пеано Þ
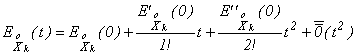 ; (3.4.1)
; (3.4.1)
![]() (по свойству 2
характеристической функции).
(по свойству 2
характеристической функции).
Далее по свойству 3 характеристической функции Þ
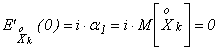 ;
;
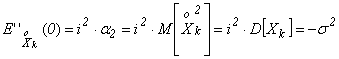
Подставим полученные значения производных в (3.4.1):
![]() (3.4.2)
(3.4.2)
II этап. Так как Þ {по свойству 5 характеристической
функции} Þ
Þ {по свойству 5 характеристической
функции} Þ
Þ  {подставляем (3.4.2)}
=
{подставляем (3.4.2)}
=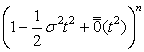
III этап. ![]() { по свойству 4 характеристической функции} =
{ по свойству 4 характеристической функции} = 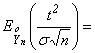
=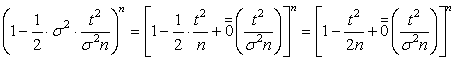
Итак, 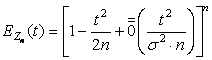 Þ.
Þ.![]()
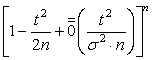 =
=
={![]() ,
, ![]() - малое} =
- малое} =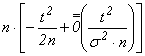 Þ
Þ 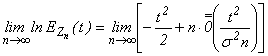 =
=
![]()
Обратимся
теперь к более тонкому и сложному вопросу об оценке погрешности нормального
приближения в интегральной теореме Муавра-Лапласа. Ранее уже говорилось, что
точной формулы для указанной погрешности не существует. Однако оказывается, что
можно получить оценку для так называемой предельной абсолютной погрешности для
любого промежутка.
Современные исследования по уточнению ЦПТ для конечных n приводят к следующему результату.
Оставаясь в рамках формулировки ЦПТ, данной нами выше (теорема 3.2.1 для
одинаково распределенных слагаемых) и сохраняя введенные там обозначения,
потребуем дополнительно существования у членов последовательности ![]() третьего абсолютного
момента. Обозначим
третьего абсолютного
момента. Обозначим ![]() .Тогда
.Тогда ![]() справедливо следующее
неравенство (известное в литературе как неравенство Берри-Эссена [4]):
справедливо следующее
неравенство (известное в литературе как неравенство Берри-Эссена [4]):
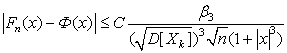 , (3.4.3)
, (3.4.3)
где ![]() - точная функция
распределения для стандартизованной суммы, а
- точная функция
распределения для стандартизованной суммы, а ![]() - некоторая абсолютная
константа, которая последовательно уточнялась в работах главным обоазом
российских математиков, и удовлетворяет неравенству
- некоторая абсолютная
константа, которая последовательно уточнялась в работах главным обоазом
российских математиков, и удовлетворяет неравенству
![]() (3.4.4)
(3.4.4)
Неравенства (3.4.3) и (3.4.4) позволяют установить величину предельной
абсолютной ошибки, допускаемой при использовании интегральной теоремы
Муавра-Лапласа.
Пример 3.4.1. Пусть ![]() подчиняется закону
подчиняется закону ![]() ,
, ![]() . Обозначим
. Обозначим
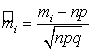 ,
, ![]() =1,2;
=1,2;
![]() -
-
точное значение искомой вероятности попадания биномиальной случайной
величины на промежуток ![]() ;
; ![]() - приближенное
значение той же вероятности, вычисленное в предположении нормальности
- приближенное
значение той же вероятности, вычисленное в предположении нормальности ![]() . Показать, что справедлива следующая оценка:
. Показать, что справедлива следующая оценка:
 (3.4.5)
(3.4.5)
где 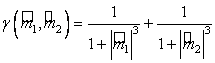
◄ Воспользуемся представлением ![]() , где
, где ![]() - индикатор успеха в
- индикатор успеха в ![]() -м опыте, причем для последовательности
-м опыте, причем для последовательности ![]() выполняются все
условия ЦПТ. ►
выполняются все
условия ЦПТ. ►
Используя закон распределения индикатора ![]() :
: ![]()
![]()
находим:
![]() ,
,
![]()
Подставляя полученные характеристики в правую часть неравенства (3.4.1) и
учитывая (3.4.2), получаем:
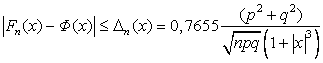 (3.4.6)
(3.4.6)
Используя свойства модуля, распишем левую часть часть в (3.4.6):
![]()
![]()
![]() ,
,
где ![]() определяется формулой
(3.4.6). Обозначая
определяется формулой
(3.4.6). Обозначая
![]() , получаем требуемый результат (3.4.5).►
, получаем требуемый результат (3.4.5).►
Полученная в примере величина ![]() имеет смысл предельной
абсолютной погрешности нормальной аппроксимации биномиальной вероятности
попадания на промежуток
имеет смысл предельной
абсолютной погрешности нормальной аппроксимации биномиальной вероятности
попадания на промежуток ![]() . Она дает лишь грубую оценку сверху для абсолютной
погрешности нормального приближения при достаточно больших значениях
. Она дает лишь грубую оценку сверху для абсолютной
погрешности нормального приближения при достаточно больших значениях ![]() и используется на
практике для получения гарантированных оценок (истинная величина абсолютной
ошибки всегда меньше полученной предельной ошибки).
и используется на
практике для получения гарантированных оценок (истинная величина абсолютной
ошибки всегда меньше полученной предельной ошибки).
Пример 3.4.2. В условиях примера 3.3.7 вычислить предельные абсолютную и относительную
погрешности нормального приближения для указанных промежутков.
◄ а) Для промежутка [15,35] вычислим нормированные значения концов интервала:
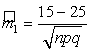 =
=![]() =
=![]() ,
, ![]() 2,3095; Отсюда следует:
2,3095; Отсюда следует:
![]() 0,15; Далее по формуле (3.4.5) получаем:
0,15; Далее по формуле (3.4.5) получаем:
![]() 0,7655
0,7655![]() =0,01657.
=0,01657.
Учитывая точное значение ![]() =0,9852, взятое из таблицы 3.3.2, получаем предельную
относительную ошибку для данного промежутка
=0,9852, взятое из таблицы 3.3.2, получаем предельную
относительную ошибку для данного промежутка ![]() 1,68%, в то время как истинное значение относительной ошибки,
указанное в той же таблице равно 0,62%.►
1,68%, в то время как истинное значение относительной ошибки,
указанное в той же таблице равно 0,62%.►
б) Промежуток [20,30]. Ответ: 0,087;
![]() =18,39%.
=18,39%.
в)
Промежуток [30,40]. Ответ: ![]() =0,417;
=0,417; ![]() =0,046;
=0,046; ![]() =30,88%.
=30,88%.
Пример 3.4.3. Вероятность выпуска микросхемы с
дефектом равна 0,03. На контроль поступила партия из 2000 микросхем. Пусть ![]() - число дефектных микросхем
в данной партии. Вычисляется вероятность события
- число дефектных микросхем
в данной партии. Вычисляется вероятность события ![]() с помощью интегральной
теоремы Муавра-Лапласа. Какую предельную абсолютную (и относительную) ошибку мы
при этом допускаем?
с помощью интегральной
теоремы Муавра-Лапласа. Какую предельную абсолютную (и относительную) ошибку мы
при этом допускаем?
◄ По
условиям данного эксперимента ![]() =0,03,
=0,03, ![]() =2000,
=2000, ![]() =60,
=60, ![]() =7,6289. (все вычисления проводятся с 4 верными знаками после
запятой). Преобразуя неравенство под знаком
=7,6289. (все вычисления проводятся с 4 верными знаками после
запятой). Преобразуя неравенство под знаком ![]() к неравенству для
стандартизованной случайной величины
к неравенству для
стандартизованной случайной величины ![]() , получаем:
, получаем:
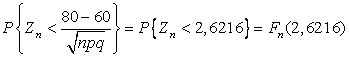 .
.
Далее по
формуле (3.4.6) при ![]() =2,6216 находим:
=2,6216 находим: ![]() =0,0052.
=0,0052.
Так как
точное значение искомой вероятности неизвестно, то для предельной относительной
погрешности используем формулу ![]() , где
, где
![]() =0,9956 – приближенное значение. Таким образом, получаем
=0,9956 – приближенное значение. Таким образом, получаем ![]() =0,0052 или 0,52%, что в данном случае является вполне
приемлемой гарантированной точностью.►
=0,0052 или 0,52%, что в данном случае является вполне
приемлемой гарантированной точностью.►
Пример 3.4.4. В условиях предыдущего примера
вычислить предельные абсолютную и относительную ошибки для вероятности события ![]() .
.
Ответ: ![]() =0,036;
=0,036; ![]() =3,38%.
=3,38%.
Пример 3.4.5. Каково гарантированное число
опытов, которые необходимо провести по схеме Бернулли с вероятностью успеха в
одном опыте ![]() =1/2, чтобы предельная абсолютная погрешность нормального
приближения для вероятности события
=1/2, чтобы предельная абсолютная погрешность нормального
приближения для вероятности события ![]() не превосходила 0,01?
Рассмотреть два случая:
не превосходила 0,01?
Рассмотреть два случая:
1) ![]() ;
;
2) ![]() .
.
◄ 1)
Преобразуем
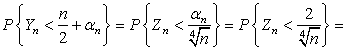
=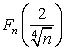 . Полагая в формуле (3.4.6)
. Полагая в формуле (3.4.6) ![]() , получаем, согласно условию,
, получаем, согласно условию,
 .
.
Учитывая,
что ![]() и отбрасывая в первом
приближении малое слагаемое в знаменателе дроби, получаем
и отбрасывая в первом
приближении малое слагаемое в знаменателе дроби, получаем ![]() 5860.►
5860.►
2) Ответ: ![]() .
.
Пример 3.4.6. Случайные величины ![]() независимы и имеют
одно и тоже геометрическое распределение с параметром
независимы и имеют
одно и тоже геометрическое распределение с параметром ![]() =1/2. Показать, что
=1/2. Показать, что
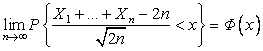 . (3.4.7)
. (3.4.7)
◄ Так
как для геометрического распределения справедливы формулы:
![]() ,
, ![]() , то согласно свойствам мат.ожидания и дисперсии, имеем:
, то согласно свойствам мат.ожидания и дисперсии, имеем: ![]() ,
, ![]() . Таким образом, для последовательности
. Таким образом, для последовательности ![]() выполнены все условия
ЦПТ. Следовательно предельным законом распределения для стандартизованной суммы
выполнены все условия
ЦПТ. Следовательно предельным законом распределения для стандартизованной суммы
![]() при
при ![]() будет нормальный
будет нормальный ![]() . Данное утверждение формулируется в терминах функции
распределения в виде равенства (3.4.7).►
. Данное утверждение формулируется в терминах функции
распределения в виде равенства (3.4.7).►
Контрольные
вопросы к главе 3
1) Пусть
для случайной величины ![]() известно только
математическое ожидание
известно только
математическое ожидание ![]() . Ответить на следующие вопросы:
. Ответить на следующие вопросы:
а) Как оценить сверху вероятность события ![]()
![]() ?
?
б) Как оценить снизу вероятность события ![]() ,
, ![]() ?
?
2) Пусть
кроме ![]() известна также
дисперсия
известна также
дисперсия ![]() . Ответить на вопросы:
. Ответить на вопросы:
а) Оценить сверху вероятность события ![]() .
.
б) Оценить снизу вероятность события ![]() .
.
3)
Определить условие, при котором применение второго неравенства Чебышева дает
лишь тривиальную оценку.
4)
Определить понятие «сходимость по вероятности».
5) Дать
определение понятию «к последовательности ![]() применим закон больших
чисел».
применим закон больших
чисел».
6)
Сформулировать теорему Чебышева.
7) Справедливо ли утверждение теоремы, если заменить
условие попарной независимости на условие попарной некоррелированности
случайной последовательности? Дать объяснение.
8)
Сформулировать закон больших чисел в частном случае одинаково распределенных
членов случайной последовательности.
9) Оценить
значение закона больших чисел в практике измерений. Показать, что средне
арифметическое ![]() независимых измерений
имеет большую относительную точность, чем у отдельного измерения.
независимых измерений
имеет большую относительную точность, чем у отдельного измерения.
10)
Сформулировать теорему Бернулли. В чем состоит значение этой теоремы для
практики измерений?
11)
Сформулировать центральную предельную теорему.
12) Оценить
значение ЦПТ в практике измерений.
13) Можно
ли заменить в ЦПТ условие независимости в совокупности на условие попарной
независимости?
14)
Сформулировать локальную теорему Муавра-Лапласа.
15)
Сформулировать интегральную теорему Муавра-Лапласа.
16) Каков
порядок погрешности нормального приближения для точных биномиальных
вероятностей попадания на промежуток при конечном ![]() ?
?
17) Как
применить интегральную теорему Муавра-Лапласа для оценки вероятностей того или
иного отклонения относительной частоты успехов в ![]() опытах от вероятности
успеха в одном опыте?
опытах от вероятности
успеха в одном опыте?
18) В чем
состоит поправка Феллера для уточнения нормального приближения в интегральной
теореме Муавра-Лапласа?
19)
Сформулировать свойство нормальной асимптотики закона Пуассона.
20)
Сформулировать свойство нормальной асимптотики закона хи-квадрат.
21) На чем
основано доказательство центральной предельной теоремы?
22) Дать
определение понятию предельная абсолютная погрешность нормального приближения в
интегральной теореме Муавра-Лапласа.
23) Написать
формулу для предельной абсолютной погрешности нормального приближения для
биномиальных вероятностей.